Vi proponiamo un gioco da fare a coppie.
Servono due dadi e due tabelle (una per ciascun giocatore) con i numeri da 1 a 12, ciascuno ripetuto due volte.
Ogni turno consiste nel tiro dei due dadi, simultaneamente, da parte di un giocatore.
Al proprio turno il giocatore può cancellare dalla propria tabella, in alternativa, o i due numeri usciti o il numero che è somma dei due numeri usciti.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Facciamo un esempio per spiegarci meglio; con il tiro 1 ∼ 2 si potrebbe cancellare una (soltanto una!) delle seguenti combinazioni:
- i due numeri 1 e 2;
- il solo numero 3.
Sta al giocatore decidere quale combinazione gli conviene utilizzare.
Se poi ottiene questa combinazione in un momento della partita in cui ha già cancellato tutti i numeri 1, allora potrà cancellare un solo numero 2 oppure un solo numero 3; se la ottiene in un momento in cui ha già cancellato i numeri 1 e 3, allora potrà cancellare un solo numero 2 . E se ha già cancellato tutti i numeri 1, 2 e 3, non potrà cancellare nulla e dovrà passare i dadi all’avversario.
Vince chi riesce per primo a cancellare tutti i 24 numeri della propria tabella.
In classe, fate almeno un paio di partite a coppia, conservando tutte le tabelle, soprattutto quelle dei giocatori che non hanno vinto.
Osservate i numeri che sono rimasti da cancellare nelle tabelle dei giocatori che non hanno vinto: c’è un numero particolarmente frequente?
Avreste potuto prevedere questo fenomeno?
Riuscite a quantificare la probabilità che, tirando due dadi come in questo gioco, il giocatore si trovi nelle condizioni di poter cancellare il numero 1? E il numero 2? E tutti gli altri numeri fino a 12?
Soluzione
Chiaramente non è possibile, prima di iniziare una partita, sapere quale giocatore vincerà, né quali numeri rimarranno da cancellare ai giocatori che perderanno. Più partite si fanno e più tabelle si collezionano, però, più salta all’occhio il fatto che è facile che tra i numeri che rimangono da cancellare a fine partita ci sia il 12.
Si può prevedere questo fenomeno perché, in effetti, l’unico caso in cui si può cancellare il 12 è con un tiro in cui esca su entrambi i dadi il numero 6; mentre per cancellare il 6 va bene qualunque tiro in cui in uno dei due dadi esce 6 e poi anche un tiro in cui esca su un dado 1 e su un altro 5, o su uno 2 e sull’altro 4, oppure….
Per quantificare la probabilità, esaminando tutti i casi possibili e indicando con P(n) la probabilità che il giocatore di turno si trovi nelle condizioni di poter cancellare il numero n, si ha:
- P(1) = 11/36
- P(2) = 12/36
- P(3) = 13/36
- P(4) = 14/36
- P(5) = 15/36
- P(6) = 16/36
- P(7) = 6/36
- P(8) = 5/36
- P(9) = 4/36
- P(10) = 3/36
- P(11) = 2/36
- P(12) = 1/36
Un problema significativo
Il gioco che si propone ai ragazzi è semplice ed è senza dubbio alla loro portata. Questa semplicità, però, non rende il problema banale: esso infatti va a toccare – in un contesto che le riempie di significato – alcune delle idee chiave di quegli argomenti di probabilità che si presentano usualmente ai ragazzi nella scuola secondaria di primo grado.
Eventi non equiprobabili
Il dado “cubico”, con le facce numerate da 1 a 6, è un oggetto che diventa spesso protagonista di esercizi, quesiti e problemi sul calcolo delle probabilità, sia perché è conosciuto da tutti (è onnipresente nei giochi in scatola!) sia perché è facilmente intuibile che, nel lancio di un dado, un qualsiasi numero da 1 a 6 ha la stessa probabilità di uscita di ciascuno degli altri numeri e che quindi questa probabilità è uguale a ⅙.
Il gioco che qui proponiamo, invece, mette in luce l’esistenza di eventi che (pur essendo tutti aleatori, casuali, imprevedibili) non hanno tutti la stessa probabilità di verificarsi, non sono tutti equiprobabili.
Non è scontato che un alunno della scuola del primo ciclo abbia già interiorizzato l’esistenza di eventi casuali più o meno probabili: discorrendo con i ragazzini spesso si ha l’impressione che distinguano bene tra eventi certi, impossibili e incerti, ma anche che mettano questi ultimi in un unico grande calderone. Ad esempio, questa è la risposta di un alunno di terza media ad un compagno che gli proponeva di pensare una strategia prima di iniziare a tirare i dadi:
Che importa? Tanto tutti i numeri escono a caso: un numero vale l’altro, sono tutti uguali! Se non hai modo di sapere che numero uscirà, è inutile che ti poni il problema di decidere cosa cancellare prima e cosa tenere per dopo!
Facendo qualche partita e soprattutto confrontando i numeri rimasti da cancellare sulle tabelle dei giocatori che hanno perso, gli alunni si convincono, ancor prima di fare i conti, che in questo gioco i numeri “non sono tutti uguali”. Questo è il primo passo indispensabile per poter avere comportamenti razionali di fronte a eventi incerti: riconoscere che, anche se non possiamo dire nulla di certo rispetto a cosa accadrà, possiamo comunque dire qualcosa e agire di conseguenza.
Eventi non incompatibili
Gli eventi su cui si concentra l’attenzione attraverso questo problema non sono tra loro incompatibili, cioè non si escludono a vicenda e per questo motivo la somma delle probabilità P(1), P(2), P(3)… fino a P(12) è maggiore di 1.
Questo può essere un motivo di difficoltà e di iniziale sconcerto perché gli esempi visti dai ragazzi sono in genere più facilmente esempi di eventi incompatibili. Pensiamo al tiro di un dado: i diversi esiti, da 1 a 6, non solo sono equiprobabili, ma sono anche incompatibili, se esce l’uno non esce l’altro, e per questo possiamo dire che la probabilità di ciascuno è 1/6.
Ad essere mutuamente esclusivi sono quelli che chiameremo gli “esiti” dei dadi, ossia le coppie ordinate di numeri che si leggono sui dadi: se ad un certo lancio escono i numeri 3 e 4, non possono contemporaneamente uscire i numeri 2 e 5! E, in effetti, questi esiti possibili, fra loro incompatibili, ed equiprobabili, sono 36, la probabilità di ciascuno di essi è 1/36 e la somma di queste 36 probabilità è 1.Ma, pe r rimanere in questo esempio, a seguito dell’esito “3 e 4” il giocatore può cancellare sia il numero 3 che il numero 4, senza che una cosa escluda l’altra.
Strategie risolutive diverse
Se agli alunni è già stata data la definizione classica di probabilità di un evento, come rapporto tra il numero dei casi favorevoli al suo verificarsi e il numero dei casi possibili, è facile che tutti i gruppi lavorino in questa direzione. Ma è anche possibile (soprattutto se su questo tipo di approccio non si è già insistito) che emergano altri modi di valutare la probabilità:
- qualche gruppo potrebbe decidere di effettuare altri lanci dei due dadi e segnarsi, di volta in volta, quali numeri si potrebbero cancellare dalla tabella, per poi andare a calcolare la frequenza con la quale compare ciascun numero rispetto al totale dei lanci effettuati;
- qualche gruppo potrebbe attribuire un certo grado di probabilità ai diversi numeri esclusivamente sulla base dell’esperienza personale avuta nella fase di gioco, magari distinguendo soltanto tra numeri “poco probabili”, “mediamente probabili” e “molto probabili”.
Stategie come quelle qui descritte, che abbiamo visto in atto in alcune delle classi che hanno affrontato questo problema, vanno apprezzate ed evidenziate, perché ci possono condurre a una riflessione sull’approccio alla probabilità di tipo frequentista e di tipo soggettivo, sulle situazioni in cui questi approcci possono essere utili e sulle accortezze da usare affinché ci portino a risultati significativi.
l’approccio classico
La difficoltà più grande che, giustamente, i ragazzi riscontrano nel quantificare in modo classico la probabilità che si verifichi un evento che rende possibile cancellare il numero n sta nel determinare quali e quanti sono i “casi possibili”, ossia quali e quanti sono i possibili esiti che si ottengono dal lancio di due dadi.
Alcuni alunni individuano 12 casi possibili, perché guardano ai numeri che è possibile cancellare: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11 e 12. Confondono, in questo modo, i diversi possibili esiti del lancio di due dadi con gli effetti di uno di tali lanci (e quindi i diversi numeri che si possono cancellare dopo un dato tiro). In questo caso gli studenti vanno aiutati a riconoscere che ci sono risultati (ad esempio: “puoi cancellare il numero 12”) che corrispondono ad un unico esito (nell’esempio precedente “esce 6 su entrambi i dadi”); ma ci sono anche risultati (ad esempio: “puoi cancellare il numero 7”) che corrispondono a ben più di un esito (nell’esempio precedente “esce 3 su un dado e 4 sull’altro”, “esce 2 su un dado e 5 sull’altro”, “esce 1 su un dado e 6 sull’altro”, …).
Altri alunni individuano 21 casi possibili, non riconoscendo la diversità di esiti del tipo: “esce 2 sul primo dado e 1 sul secondo” ed “esce 1 sul primo dado e 2 sul secondo”. Si tratta di un errore “classico”, potremmo anche dire (e potremmo dirlo anche ai nostri alunni) che si tratta di una misconcezione storica, di una convinzione che è perdurata fino al Rinascimento. I primi a rendersi conto che gli esiti da considerare in un gioco come questo sono 36 e non 21 furono Gerolamo Cardano, nel Liber de ludo aleae (scritto nel 1564 ma pubblicato solo nel 1663), e Galileo Galilei, nel breve saggio Sopra le scoperte dei dadi (scritto tra il 1612 e il 1623). In realtà Cardano e Galilei si sono occupati del lancio di tre dadi, come avveniva nel gioco della zara, ma il problema è del tutto analogo.
Un lungo elenco
Un modo “pedante” ma convincente, per contare gli esiti possibili e quelli favorevoli al verificarsi di un certo risultato è quello di elencarli tutti.
Se qualche gruppo di ragazzini si cimentasse in questa impresa dovremmo incoraggiarli, qualsiasi sia la strada che essi imboccano, esortandoli a trovare un modo per essere sicuri di non tralasciare alcun caso. Durante la discussione finale, se anche ai ragazzi non fosse venuto in mente questo sistema, si può mostrare loro una tabella a doppia entrata che, in modo molto efficace, rappresenta in poco spazio tutti i casi possibili.
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 1, 2 | 1, 2, 3 | 1, 3, 4 | 1, 4, 5 | 1, 5, 6 | 1, 6, 7 |
| 2 | 1, 2, 3 | 2, 4 | 2, 3, 5 | 2, 4, 6 | 2, 5, 7 | 2, 6, 8 |
| 3 | 1, 3, 4 | 2, 3, 5 | 3, 6 | 3, 4, 7 | 3, 5, 8 | 3, 6, 9 |
| 4 | 1, 4, 5 | 2, 4, 6 | 3, 4, 7 | 4, 8 | 4, 5, 9 | 4, 6, 10 |
| 5 | 1, 5, 6 | 2, 5, 7 | 3, 5, 8 | 4, 5, 9 | 5, 10 | 5, 6, 11 |
| 6 | 1, 6, 7 | 2, 6, 8 | 3, 6, 9 | 4, 6, 10 | 5, 6, 11 | 6, 12 |
Nella colonna e nella riga di intestazione si trovano i numeri che possono comparire sul primo e sul secondo dado rispettivamente; nelle celle interne si trovano i numeri che si possono cancellare in corrispondenza dei vari lanci. Ad esempio: all’incrocio fra la riga del 2 e la colonna del 3 si trovano i numeri che si possono cancellare dopo un lancio dei dadi il cui esito sia un 2 sul primo dado e un 3 sul secondo dado.
Gli esiti possibili sono quindi 36.
11 delle celle interne della tabella contengono il numero 1, quindi 11 dei 36 esiti danno la possibilità di cancellare il numero 1: la probabilità che il giocatore di turno si trovi nelle condizioni di poter cancellare il numero 1 è P(1) = 11/36.
Dagli analoghi conteggi per i numeri da 2 a 12 si ottiene che P(2) = 12/36, P(3) = 13/36, P(4) = 14/36, P(5) = 15/36, P(6) = 16/36, P(7) = 6/36, P(8) = 5/36, P(9) = 4/36, P(10) = 3/36, P(11) = 2/36 e P(12) = 1/36.
Qualche riflessione
Nelle classi in cui questo problema è stato proposto abbiamo visto alcuni alunni calcolare (dopo aver contato gli esiti favorevoli e quelli possibili) le precedenti P(1), P(2), P(3) e convincersi che la probabillità P(n) andasse crescendo con n, aumentando sempre di 1!
Di fronte a una situazione simile, è importante far riflettere i ragazzi sul fatto che conoscere i primi termini di una lista di numeri non è mai condizione sufficiente per determinare gli altri numeri: occorre conoscere la “regola” che genera i numeri, e regole diverse potrebbero dare luogo a liste che iniziano nello stesso modo ma poi si diversificano notevolmente.
Il modo più efficace per condurli a questa riflessione è lasciarli andare avanti, fino a che si accorgono dell’errore (e non possono non accorgersene perché, di questo passo, P(12) sarebbe 22/36, in particolare sarebbe la probabilità più grande, mentre i ragazzi avranno sperimentato che 12 è il numero più duro da cancellare)!
Ci sono anche ragazzi, però, che si accorgono del perché le probabilità sono così diverse e riescono, per così dire, a trovare la “regola” per calcolarle (e anche a spiegare agli altri cosa hanno visto e cosa hanno fatto).
Nelle classi in cui il problema è stato sperimentato, alcuni ragazzini hanno fatto le seguenti osservazioni a posteriori, dopo aver contato i vari esiti elencati in una tabella simile a quella costruita qui sopra; altri alunni, invece, troppo pigri per costruire la tabella con tutti i casi possibili e troppo svegli per cadere in facili tranelli, le hanno fatte addirittura a priori e hanno calcolato grazie ad esse il numero dei casi possibili e dei casi favorevoli:
- ogni numero da 1 a 6 può essere cancellato quando compare sulla faccia di un dado; questo dà origine a 11 esiti favorevoli: 6 relativi a quando compare sul primo dado e 5 relativi a quando compare sul secondo dado (dovrebbero essere 6, ma uno lo si è già contato quando compare in concomitanza anche sul primo dado);
- il numero 1 non può essere ottenuto come somma di due numeri naturali tra 1 e 6, quindi P(1) = 11/36;
- i numeri da 2 a 6 possono essere cancellati anche come somme dei numeri che compaiono sulle facce dei due dadi; il numero 2 si può ottenere come somma in corrispondenza dell’unico esito (1, 1), il numero 3 in corrispondenza di due esiti ((1, 2) e (2, 1)), il numero 4 di tre esiti ((1, 3), (3, 1) e (2, 2)), il numero 5 di quattro esiti ((1, 4), (4, 1), (2, 3) e (3, 2)) e il numero 6 di cinque esiti ((1, 5), (5, 1), (2, 4), (4, 2), (3, 3));
- quindi
P(2) = (11+1)/36 = 12/36
P(3) = (11+2)/36 = 13/36
P(4) = (11+3)/36 = 14/36
P(5) = (11+4)/36 = 15/36
P(6) = (11+5)/36 = 16/36 - i numeri da 7 a 12 non possono comparire direttamente sulla faccia di un unico dado: possono essere cancellati solo come somme dei numeri che compaiono sulle facce dei due dadi;
- il numero 7 si può ottenere come somma in corrispondenza di sei esiti ((1, 6), (6,1), (2, 5), (5, 2), (4, 3) e (3, 4)), il numero 8 in corrispondenza di cinque esiti ((2, 6), (6, 2), (3, 5), (5, 3) e (4, 4)), il numero 9 di quattro esiti ((3, 6), (6, 3), (4, 5) e (5, 4)), il numero 10 di tre esiti ((4, 6), (6, 4) e (5, 5)), il numero 11 di due esiti ((5, 6) e (6, 5)) e il numero 12 dell’unico esito (6, 6);
- quindi
P(7) = 6/36
P(8) = 5/36
P(9) = 4/36
P(10) = 3/36
P(11) = 2/36
P(12) = 1/36.
Una pigrizia sana, questa, che ha spinto dei ragazzini a fare un lavoro anche più consistente e certo più significativo rispetto al mero elenco dei casi possibili, e che ci fa tornare in mente questa frase di George Pólya:
La matematica è essere pigri. La matematica è far sì che i principi facciano il lavoro per te così che tu non lo debba fare per conto tuo.
Un problema memorabile
A rendere memorabile questo problema è, senza ombra di dubbio, il gioco che lo precede. Si tratta di un gioco semplice: sono semplici le regole, è semplice il materiale occorrente, è semplice il susseguirsi delle azioni. Eppure è un gioco che entusiasma, cattura e diverte, creando così delle ottime condizioni per l’apprendimento.
Sperimentazione e possibili scenari
Il gioco da cui prende vita questo problema è stato presentato dalla professoressa Anna Asti durante il corso MathUp “Noi la insegniamo così” per la scuola secondaria di primo grado nell’anno scolastico 2020 / 2021, riprendendo un laboratorio proposto presso il Centro matematita.
Non richiede particolari prerequisiti, se non il concetto di rapporto tra numeri interi (che non è altro che il concetto di frazione), quindi può essere proposto agli alunni di terza media, ma anche agli alunni delle classi precedenti. Quella di dedicare un po’ di tempo alla probabilità soltanto in terza media è una abitudine che può tranquillamente essere mantenuta (a patto di non far pensare ai ragazzi che abbiano bisogno di chissà quali strani strumenti per affrontare questo tema), ma può essere anche abbandonata! Introdurre qualche problema sulla probabilità già in prima o in seconda può essere utile per creare più momenti, distanziati nel tempo, in cui parlare di incertezza, ma anche per fornire un esempio “concreto” di una situazione in cui il concetto di rapporto (o di frazione) entra in gioco in modo pieno di significato.
Un gioco con i dadi per i primi anni di scuola primaria
Non è mai troppo presto per iniziare a far riflettere i bambini sul fatto che, a volte, non abbiamo abbastanza elementi per poter prevedere con certezza quale sarà la conseguenza di una nostra azione e che, ciò nonostante, possiamo comunque prendere delle decisioni razionali, anche in base a valutazioni di tipo quantitativo.
Non si tratta certo di anticipare il “calcolo delle probabilità” alla scuola primaria, così come non c’è motivo per anticipare alcun altro tecnicismo. Si può però cominciare, fin dai primi anni della scuola primaria, a ragionare sulle situazioni di incertezza, e lo si può fare attraverso un gioco simile a quello sopra presentato, che non richiede però nemmeno di saper sommare i numeri che compaiono sui dadi. Questo gioco è stato presentato da Anna Asti in uno dei Venerdì di MathUp, un ciclo di webinar rivolti ad insegnanti della scuola del primo ciclo, tenuti da mateinitaly nell’anno scolastico 2020 / 2021. È stato poi ripreso nell’articolo Quantificare l’incertezza comparso sul numero 7 della rivista Focus Scuola (luglio 2021).
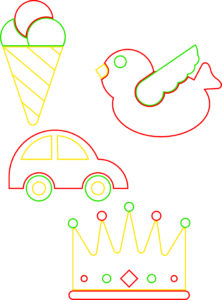
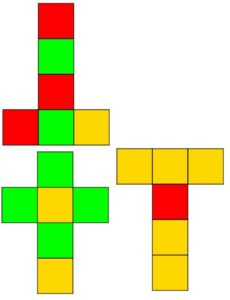
Si gioca a coppie. Ogni coppia ha a disposizione un foglio con i disegni riportati qui sotto a sinistra e tre dadi che si possono costruire a partire dagli sviluppi piani sulla destra.
A un giocatore spetta il compito di colorare il cono gelato e l’automobile, all’altro quello di colorare la corona e l’uccellino. Dopo essersi distribuiti i compiti, i giocatori si alternano nel tirare un dado e nel colorare, su uno dei propri disegni, una sola delle zone contornate dal colore uscito sul dato. Il giocatore di turno può decidere quale dado tirare. Vince il primo che termina di colorare entrambi i propri disegni.
Di seguito, riportiamo alcune delle domande che si possono porre ai bambini e discutere con loro, dopo averli lasciati giocare!
- Il giocatore a cui tocca colorare il cono gelato e l’automobile deve colorare lo stesso numero di parti che spettano a colui che deve colorare la corona e l’uccellino? (Sì, sono 16 parti in ogni caso).
- I due giocatori devono colorare lo stesso numero di parti per ciascun colore? (No. Al giocatore che deve colorare il cono gelato e l’automobile spettano 2 parti rosse, 10 parti gialle e 4 parti verdi. A giocatore che deve colorare la corona e l’uccellino spettano 7 parti rosse, 2 parti gialle e 7 parti verdi).
- Quale dado conviene tirare (all’inizio del gioco) al giocatore che deve colorare il cono gelato e l’automobile? Lanciando questo dado è sicuro di vincere? (Dovendo colorare così tante parti gialle, a questo giocatore converrà tirare il dado con più facce gialle, anche se questo non gli dà la certezza di vincere).
- Quale dado conviene tirare (all’inizio del gioco) al giocatore che deve colorare la corona e l’uccellino? Lanciando questo dado è sicuro di vincere? (Dovendo colorare così tante parti rosse e verdi, a questo giocatore converrà tirare i dadi con più facce di questi colori, pur sapendo di non avere nemmeno così la certezza di vincere).
- Supponiamo che ciascun giocatore debba scegliere un unico dado e lanciare sempre quello. C’è un dado scegliendo il quale il giocatore che deve colorare il cono gelato e l’automobile è sicuro di vincere? C’è un dado scegliendo il quale è sicuro di perdere? E il giocatore che deve colorare la corona e l’uccellino? (Val la pena far riflettere i bambini sul fatto che, se è opportuno e razionale scegliere bene il dado da tirare, è anche vero che in giochi come questi c’è sempre una imprevedibilità legata al caso. Vero è, però, che entrambi i giocatori, se scegliessero di giocare lanciando solo il dado senza alcuna faccia rossa, si metterebbero in condizione di non poter finire di colorare i propri disegni).
Materiale necessario
Due dadi classici, a sei facce, possibilmente diversi tra loro (per colore, o dimensioni, o per come sono scritti i numeri): la diversità dei dadi aiuta i ragazzi a distinguere l’esito di un dado da quello dell’altro.
Un foglio su cui scrivere la tabella (si può utilizzare il file “Schema di gioco” allegato in fondo a questo articolo).




un lavoro veramente esemplare da tutti i punti di vista: vale un intero corso su come insegnare la probabilità. Tutti i materiali sono comunque interessanti. Il sito è una “miniera d’oro” per la didattica della matematica
Gentilissima professoressa, grazie!
Non sta a noi darle ragione, ovviamente, ma sicuramente quello che stiamo cercando di fare è propri questo: non solo condividere i testi dei bei problemi che ci sono capitati sotto mano e che abbiamo proposto in classe (magari rivisti alla luce della esperienza nostra e di altri colleghi), ma fornire anche spunti che possano aiutare ogni docente a riflettere sul proprio modo di insegnare, a diventare consapevole delle proprie scelte didattiche, ad aprirsi a modi diversi di approcciare la matematica insieme agli alunni.
Questa mattina ho proposto questo gioco. È stato un successo!
Le argomentazioni e osservazioni portate dai ragazzi in linea con le descrizioni che avete riportato.
Bene, Marcella, ci fa proprio piacere!