Un giorno, Bernardo, Giorgio e Riccardo riuscirono a entrare di nascosto nel cortile del castello di Re Infinito. Il loro sguardo fu subito attratto da due scatole ben sigillate, una color rosso rubino e l’altra color verde smeraldo.
Leggi tutto “Nel castello di Re Infinito”
Scherzi di capodanno
Nel dicembre 2021 a Ulcinj (Dulcigno), in Montenegro, è stata montata una decorazione stradale per festeggiare l’arrivo del nuovo anno. Pare che alcuni baldi giovani di notte abbiano cambiato la posizione delle cifre luminose, sicché al mattino gli abitanti di Dulcigno si sono improvvisamente trovati ad attendere il 2202, con un balzo in avanti nel tempo di 180 anni!
Leggi tutto “Scherzi di capodanno”
Allegati
Un gioco con i dadi
Vi proponiamo un gioco da fare a coppie.
Servono due dadi e due tabelle (una per ciascun giocatore) con i numeri da 1 a 12, ciascuno ripetuto due volte.
Ogni turno consiste nel tiro dei due dadi, simultaneamente, da parte di un giocatore.
Al proprio turno il giocatore può cancellare dalla propria tabella, in alternativa, o i due numeri usciti o il numero che è somma dei due numeri usciti.
Leggi tutto “Un gioco con i dadi”
Allegati
Prismi, piramidi e altro
Questo è un problema che potreste esplorare anche a occhi chiusi, cercando di esercitare la vostra fantasia, e discutendo fra di voi in modo da usare l’immaginazione di tutti. Pensiamo però che a un certo punto vi sarà utile aprire gli occhi e provare a costruire qualche oggetto.
Leggi tutto “Prismi, piramidi e altro”
Allegati
Costruire un pallone da calcio
Per condividere con gli alunni il video che presenta questo problema, fornire il seguente link:
https://youtu.be/lNfwicOaAHs
Domande e risposte
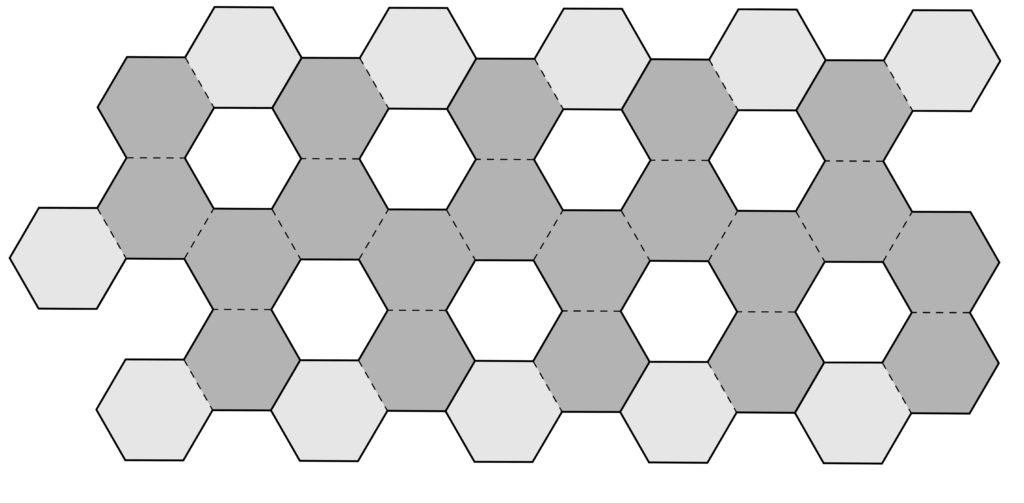
A partire dal reticolo esagonale allegato a fondo pagina (citato nel video come “il disegno di Simone”) è possibile costruire un solido che ricorda un pallone da calcio.
Quante facce esagonali ha questo solido? E quante pentagonali?
Il solido che si ottiene nel video e che assomiglia a un pallone da calcio ha 20 facce esagonali e 12 “buchi” pentagonali, in corrispondenza di ciascuno dei quali possiamo immaginare una faccia.
Quanti esagoni ci sono nel reticolo del disegno di Simone?
Nel reticolo che appare sul disegno mostrato nel video si possono contare 39 esagoni, 8 dei quali vengono poi “eliminati” dai tagli lungo le linee continue.
Istruzioni
La richiesta di scrivere delle istruzioni precise, che consentano a chi non ha visto il video di ricostruire il solido, può essere soddisfatta in molti modi.
Dalle istruzioni deve emergere il fatto che alcuni esagoni vanno incollati su altri esagoni, lasciando dei “buchi” a forma di pentagono. Come suggerito nel video, indicare sullo stesso disegno quali esagoni vadano incollati su quali altri potrebbe facilitare di molto le cose.
Commenti
Un problema significativo
Immaginare a occhi chiusi, costruire a occhi aperti
Spesso, nella scuola, si parla della necessità di sviluppare le capacità di visualizzazione spaziale degli alunni. Particolarmente rilevante è, a questo proposito, la capacità di pensare il solido che si può costruire a partire da un certo sviluppo piano. Questa abilità può essere allenata attraverso varie esperienze concrete, purché sempre accompagnate da opportune riflessioni: costruire solidi a partire dal loro sviluppo piano; disegnare lo sviluppo piano di un solido dato; individuare sviluppi piani diversi dello stesso solido; indicare – su un dato sviluppo – quali lati dei poligoni che lo compongono andranno a combaciare con quali altri lati per costruire un certo solido…
In questo problema, le abilità di visualizzazione spaziale degli alunni entrano ancor più in gioco, insieme alla immaginazione, in quanto il reticolo esagonale disegnato sul foglio di carta NON coincide con lo sviluppo piano del solido: ci sono tanti esagoni di troppo e… mancano i pentagoni!
Dove si nascondono alcuni esagoni? Da dove vengono i pentagoni? Nello scrivere le istruzioni richieste, gli alunni dovranno, in un certo senso, rispondere a queste domande.
La situazione che si presenta più frequentemente è questa: 6 esagoni disposti ad anello attorno a un settimo esagono completamente delimitato da linee continue (e che quindi diventerà un buco nel reticolo); i 6 esagoni diventano 5 perché uno di essi viene incollato su un altro e l’esagono centrale diventa un buco pentagonale.
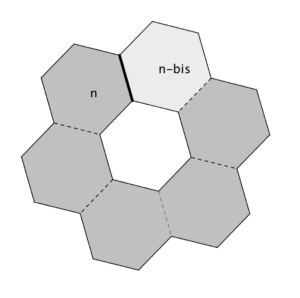
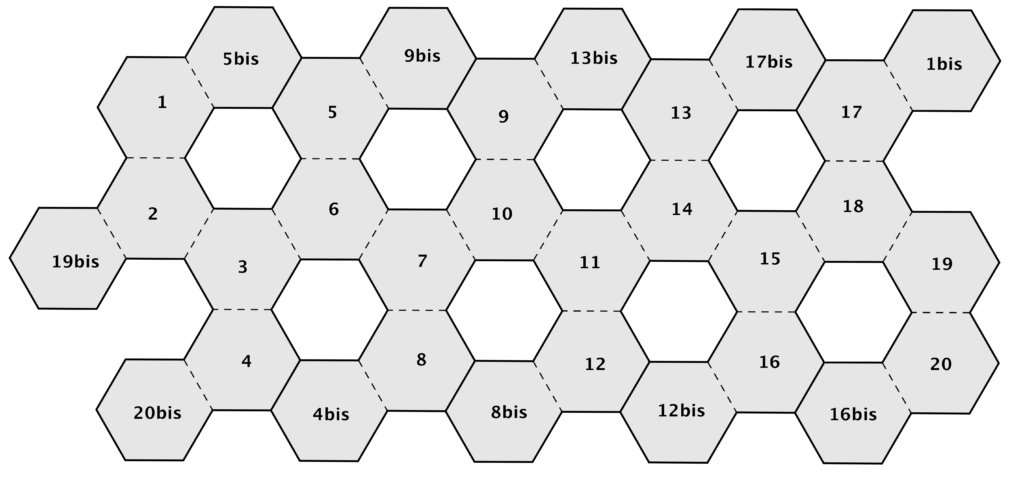
Ma ci sono anche coppie di esagoni che sul reticolo sono “lontani” e che devono essere incollati uno sull’altro: lo si capisce anche prima di aver costruito il solido, perché altrimenti non si potrebbe ottenere qualcosa che assomiglia a un pallone. Non è però facile capire di quali esagoni si tratti, se ci si limita a osservare il reticolo o a guardare il video! Dopo aver costruito il solido, però, attraverso un gioco di passaggi continui dalla manipolazione alla riflessione (e viceversa), dal pensare al toccare (e viceversa), dal costruire a occhi aperti all’immaginare a occhi chiusi (e viceversa) i ragazzi potranno concludere che gli esagoni “lontani” da incollare uno sull’altro saranno quelli indicati in FIGURA 2 con le etichette 1 e 1bis, 19 e 19bis, 20 e 20bis.
cogliere le analogie
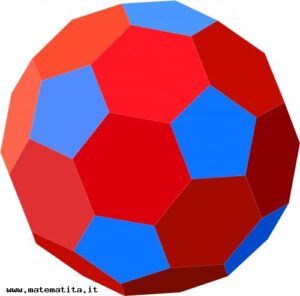
Una buona dose di immaginazione serve anche per vedere l’analogia tra il pallone da calcio e l’oggetto, pieno di buchi, che si costruisce col cartoncino, nonché tra questo oggetto e il poliedro archimedeo con 20 facce esagonali e 12 facce pentagonali che è rappresentato nella figura qui sotto.
Un problema memorabile
Tanti fattori possono rendere questo problema memorabile: lo stupore che si prova nel vedere che da un reticolo fatto di soli esagoni nasce un solido in cui si individuano anche dei pentagoni, il fatto che si parli di un oggetto tanto comune quanto amato come il pallone da calcio, il fatto che i ragazzi si scoprano capaci di costruire da soli qualcosa di veramente bello…
Ciascun insegnante, nel contesto della propria classe, saprà agganciare a questo problema discussioni, riflessioni e scoperte in modo tale che tornino facilmente alla mente degli alunni, ogni volta che rivedranno o ripenseranno a un pallone da calcio!
Un problema aperto
In questo video-problema si chiede agli alunni di contare quanti sono gli esagoni e quanti sono i buchi pentagonali nell’oggetto che si costruisce a partire dal reticolo esagonale, che è come contare gli esagoni e i pentagoni che, una volta cuciti insieme, formano un pallone da calcio; ed è anche come contare le facce del poliedro che il pallone da calcio richiama.
È probabile che, mentre cercano di risolvere questo problema, gli alunni stessi si pongano ulteriori domande ed è utile che l’insegnante le raccolga, soprattutto se intende approfondire alcune questioni.
come si chiama il poliedro corrispondente al pallone da calcio?
È sorprendente la necessità (a volte quasi impellente) che i ragazzini hanno di dare un nome agli oggetti che imparano a riconoscere. E i nomi di questo poliedro possono far nascere altre domande.
Un nome attribuito a questo poliedro è icosaedro tronco (o troncato): perché?
Una risposta “visuale” (che, a seconda dell’età degli studenti, si potrà tradurre in modo sempre più appropriato nel linguaggio della geometria) si trova nel video qui sotto, tratto dal canale YouTube Mnogogranniki Ru (un canale educativo russo, tutto dedicato ai poliedri). Nel video si mostra come questo poliedro si ottiene a partire da un icosaedro “tagliando via”, intorno a ciascuno dei 12 vertici, una piramide (che sarà a base pentagonale, perché in ogni vertice arrivano 5 facce).
Qualcuno indica questo poliedro come poliedro uniforme (5, 6, 6): perché?
Si tratta di un poliedro uniforme perché intorno a ogni suo vertice arrivano gli stessi poligoni e, inoltre, comunque si fissino due vertici, è possibile rigirare il poliedro in modo da spostare il primo nella posizione del secondo. Queste caratteristiche fanno sì che il poliedro si possa identificare con una serie di numeri che indicano (in ordine) il numero di lati delle facce che arrivano in uno stesso vertice. Il nostro poliedro dunque è un poliedro uniforme di tipo (5,6,6): in ogni vertice arrivano un pentagono regolare e due esagoni regolari.
Quanti sono gli spigoli del poliedro corrispondente al pallone da calcio?
Questa domanda equivale a chiedersi quante sono le cuciture che bisogna fare per costruire il pallone da calcio a partire da pezze esagonali e pentagonali.
Per rispondere, gli alunni possono iniziare a contare spigolo per spigolo, magari aiutandosi con un pennarello per non rischiare di contare lo stesso spigolo due volte. Non è raro, però, che (pensando al pallone da calcio e alle pezze da cucire insieme) in qualche gruppo i ragazzi si accorgano che ogni cucitura unisce due lati, di due pezze diverse. I lati delle pezze esagonali sono 20×6=120; i lati delle pezze pentagonali sono 12×5=60; i lati sono quindi in tutto 180 e le cuciture da fare saranno 180:2=90.
Quanti sono i vertici del poliedro corrispondente al pallone da calcio? C’è qualche legame tra il numero delle facce, degli spigoli e dei vertici?
Contate le facce e contati gli spigoli, si possono contare (uno alla volta, o con qualche strategia che faccia riferimento alla simmetria del poliedro) anche i vertici.
A partire da questo e da altri problemi che abbiano a che fare con il numero di facce, vertici e spigoli di un poliedro, si potranno avvicinare gli alunni alla relazione di Eulero, dando così loro l’occasione di toccare un nodo della matematica profondo e importante, di cui parleremo nella sezione Quasi un libro.
Un problema difficile
La difficoltà di questo problema, inizialmente, potrebbe sembrare di tipo manuale. In realtà i ragazzi si accorgeranno presto che la costruzione di questo solido non è più complicata di quella di tanti altri che si possono fare con cartoncino, forbici e colla: la costruzione di molti solidi, anche se apparentemente più semplici, richiede infatti maggior precisione nei tagli (perché gli angoli delle facce o tra una faccia e l’altra sono più stretti) o nella fase di incollaggio (perché le superfici da incollare sono più sottili o difficili da stringere tra le dita).
La vera difficoltà sta nello scrivere delle istruzioni che servano a qualcuno che non ha potuto vedere il video: occorre osservare bene quanto viene proposto dall’insegnante, provare a ripeterlo (probabilmente più volte) focalizzando l’attenzione sui diversi passaggi che si compiono e trovare un modo per descriverli che sia davvero utile allo scopo. Entrano qui in gioco abilità e competenze linguistiche, perché i ragazzi dovranno fare un uso appropriato ed efficace del linguaggio; ma entrano in gioco anche abilità e competenze che hanno molto a che fare con la matematica e con il pensiero computazionale, per quanto non si vedano numeri, né calcoli, né calcolatori automatici!
Un problema di matematica con effetto sorpresa
Le sorprese suscitate da questo problema possono essere tante, a seconda della classe a cui lo proponiamo.
Chi non ha mai osservato da vicino un classico pallone da calcio e non ha mai notato le cuciture che caratterizzano la sua superficie risulta sorpreso nello scoprire che non si tratta di una sfera perfetta e uniforme, bensì del risultato di tanti singoli poligoni che si inarcano verso l’esterno per effetto della pressione dell’aria interna al pallone stesso.
Molti di quelli che, invece, queste cuciture le hanno già notate si stupiscono del fatto che i singoli pezzi non sono tutti esagoni, anche se con poco sforzo (pensando alla tassellazione del piano in esagoni che si può immaginare guardando i favi di un’arnia o i pavimenti di molte cucine…) si accorgono che, con esagoni soltanto, non si può fare una palla: tre esagoni regolari posti attorno a un unico vertice si uniscono uno all’altro formando una superficie piana.
Quasi tutti si stupiscono, a buon conto, che dal reticolo di soli esagoni si possa costruire il pallone da calcio: non è facile, all’inizio, immaginare che basti lasciare dei buchi pentagonali per ottenere l’effetto desiderato!
Scenari possibili
Questo problema si presta ad essere proposto a livelli molto diversi (meglio se adeguando il tono del racconto e delle richieste all’età dei nostri interlocutori).
Per alunni della scuola primaria, potrebbe essere il coronamento di una serie di attività sui poliedri o sulla geometria solida, mentre per alunni della scuola secondaria potrebbe essere usato come avvio allo studio dei poliedri (per il primo grado) e della relazione di Eulero (per il secondo grado).
Materiale necessario
A fondo pagina è possibile scaricare il file con il reticolo di cui si parla nel video-problema.
È opportuno dare a ogni alunno questo reticolo stampato su cartoncino (quello da 120 g/m2 è dello spessore adatto), in modo da poter costruire il proprio pallone da calcio. È altrettanto opportuno che ogni alunno, o ogni gruppo, riceva qualche copia in più, stampata anche solo su carta, per poterci lavorare al fine di scrivere le istruzioni richieste.
Allegati
Affettare un cubo
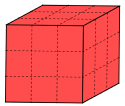
Partiamo da un cubo, coloriamone la superficie esterna di rosso e affettiamolo in cubetti, dividendo ogni spigolo in tre parti uguali, come in figura.
Siete d’accordo che i cubetti in totale sono 27 e che, fra questi, ce n’è uno solo (al centro) che non ha facce rosse, ce ne sono 6 con una sola faccia rossa, 12 con due facce rosse, 8 con tre facce rosse, e nessuno con più di tre facce rosse?
Leggi tutto “Affettare un cubo”
Allegati
Il patchwork quadrato
La nonna di Alessandra vuole confezionare una coperta quadrata, con la tecnica del patchwork, ossia unendo tramite cuciture tanti riquadri di stoffe diverse. Ha preparato 25 riquadri di stoffe di 5 colori diversi: 5 riquadri per ciascun colore.
Leggi tutto “Il patchwork quadrato”
Allegati
Il fregio di Halloween
Le maestre hanno deciso di decorare la scuola primaria di Tuttinfesta, in occasione della festa di Halloween, con un unico lunghissimo fregio che corre sulle pareti dei corridoi e delle aule.
![]()
Leggi tutto “Il fregio di Halloween”
Allegati
Cosa si può fare con cinque quadretti
Luca è arrivato in classe l’altro giorno con questi due disegni, e ci ha raccontato che il suo amico Michel, che abita a Parigi e che è venuto a trovarlo nelle vacanze di Natale, gli ha detto che nella sua classe ne hanno costruiti tantissimi per via di un problema di geometria e che poi li hanno appesi alla parete per decorare la classe.
Leggi tutto “Cosa si può fare con cinque quadretti”
Allegati
Le due automobili
Nell’automobile A ci sono due maschi; nell’automobile B ci sono un maschio e una femmina.
Vedo sfrecciare una delle due macchine, ma riesco a vedere solo un componente dell’equipaggio: è un maschio.
Leggi tutto “Le due automobili”
Allegati
Sgabelli cubici
A scuola sono arrivati un gran numero di cubi, da usare come sgabelli per una scuola materna; abbiamo a disposizione due colori, il giallo e il blu, e vogliamo colorare i cubi in modo tale che ogni faccia sia tutta dello stesso colore.
In quanti modi diversi li possiamo colorare?
Allegati
Almeno una testa!
Qual è la probabilità che lanciando 2 monete esca almeno una volta testa?
E lanciando 6 monete, qual è la probabilità che esca almeno una volta testa?
Leggi tutto “Almeno una testa!”
Allegati
Furbetti in coda
Come probabilmente vi sarà già capitato di vedere, a volte all’entrata di un negozio o di un ufficio vengono distribuiti dei numeretti per stabilire in che ordine le persone arrivate saranno servite, in modo da evitare litigi o spiacevoli discussioni.
Leggi tutto “Furbetti in coda”
Allegati
La fabbrica di saponette
Una fabbrica di saponette vuole predisporre delle casse di imballaggio che contengano ciascuna 1000 saponette.
Quali dimensioni dovranno avere queste casse se le saponette hanno (approssimativamente) la forma di un parallelepipedo che misura 3 cm x 6 cm x 9 cm?
Leggi tutto “La fabbrica di saponette”
Allegati
I due innamorati
Lui abita a Roma, Lei a Milano.
Lui ama Lei con profondo trasporto.
Anche Lei ama Lui, ma, ultimamente, in modo decisamente meno lineare e più contraddittorio.
Leggi tutto “I due innamorati”
Allegati
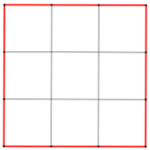
Affettare un quadrato
Partiamo da un quadrato, mettendone in evidenza i lati (in figura colorati in rosso); tagliamolo in quadratini, dividendo ogni lato in tre parti uguali; come vediamo dalla figura, dei 9 quadratini ottenuti, uno non ha lati rossi, 4 hanno un solo lato rosso, 4 ne hanno due e nessuno ne ha più di due.
Leggi tutto “Affettare un quadrato”