La nonna di Alessandra vuole confezionare una coperta quadrata, con la tecnica del patchwork, ossia unendo tramite cuciture tanti riquadri di stoffe diverse. Ha preparato 25 riquadri di stoffe di 5 colori diversi: 5 riquadri per ciascun colore.
Vuole ora cucire i riquadri di stoffa in modo tale che non siano mai vicini due riquadri dello stesso colore; e non solo vuole che non si tocchino lungo un lato, ma non vuole neppure che si incontrino in un vertice.
Vuole inoltre che in ogni riga compaiano tutti i colori e che anche in ogni colonna compaiano tutti i colori.
Prima di iniziare a cucire, cerca di disporre i riquadri secondo il criterio che si è data, ma ad ogni tentativo, prima o poi, si ritrova con due quadrati dello stesso colore che finiscono con l’essere vicini.
Riuscireste ad aiutarla?
Se la nonna avesse preparato 16 riquadri di stoffa, di cui 4 rossi, 4 blu, 4 gialli e 4 azzurri, potrebbe disporli secondo lo stesso criterio?
E se ne avesse preparati 9, di cui 3 rossi, 3 blu e 3 gialli?
Soluzione
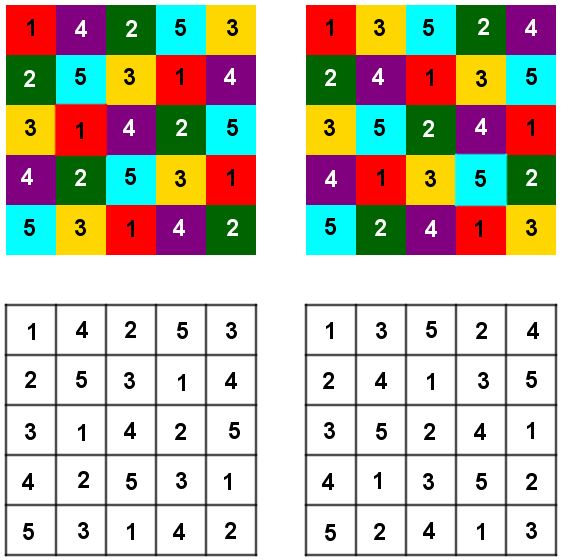
Cominciamo a disporre in un ordine qualsiasi i 5 riquadri di 5 colori diversi nella prima colonna; si verifica poi allora facilmente che questa disposizione si può completare in due modi diversi, dando origine alle due soluzioni qui di seguito rappresentate:
Se i colori a disposizione sono 3 e si hanno 3 riquadri di stoffa di ciascun colore, non si riescono a disporre in un quadrato in modo tale che due riquadri dello stesso colore non si tocchino e che su ogni riga e su ogni colonna compaiano tutti i colori; la stessa cosa accade se si hanno a disposizione 4 colori e 4 riquadri di stoffa per ciascun colore.
Commenti
Nel momento in cui devono cercare una soluzione al caso 5×5, la cosa più facile è che bambini e ragazzi procedano per tentativi ed arrivino alle soluzioni qui sopra proposte.
Anche nel caso 3×3 e in quello 4×4 possono procedere per tentativi, ma se vogliono convincersi (e convincere i loro compagni) del fatto che una soluzione non esiste, devono analizzare tutti i casi possibili. In alternativa, possono trovare una giustificazione sintetica, che potrebbe essere simile a quella che proviamo a dare qui.
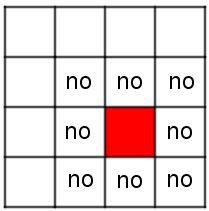
Nel caso 3×3, basta considerare la casella centrale: se abbiamo usato il rosso per questa casella, non sapremmo dove mettere gli altri due riquadri rossi, perché tutte le altre 8 caselle toccano quella centrale, o lungo uno spigolo o in un vertice.
Nel caso 4×4, guardiamo la casella all’incrocio fra la terza riga e la terza colonna; se questa è di colore rosso, abbiamo altri tre riquadri rossi da piazzare e questi possono stare solo o nella prima riga o nella prima colonna: se ce n’è uno solo nella prima riga, allora necessariamente ce ne saranno due nella prima colonna; se ce n’è uno solo nella prima colonna, allora necessariamente ce ne saranno due nella prima riga; in ogni caso non riusciamo a piazzarli rispettando le regole imposte.
Un problema significativo
Una questione che è probabile spunti in maniera naturale dal lavoro di gruppo e dal confronto tra i diversi gruppi (anche se il testo del problema non lo richiede) è il decidere quando possiamo dire che due soluzioni sono “uguali” a una delle due proposte qui sopra. Ci saranno gruppi di ragazzi che avranno usato colori diversi (che non sono il rosso, il giallo, il porpora, l’azzurro e il verde); e anche gruppi che hanno usato gli stessi 5 colori ma hanno disposto i 5 colori nella prima colonna con un ordinamento diverso da quello per esempio che abbiamo utilizzato qua. Quindi c’è da immaginare che le soluzioni trovate dai ragazzi appaiano, a prima vista, tutte diverse. Eppure… non è difficile rendersi conto (e per i ragazzi può essere proprio una bella scoperta!) che in realtà tutte le soluzioni sono “uguali” a una delle due che abbiamo qui illustrato. In che senso?
Prendiamo una soluzione che a prima vista ci sembri “diversa” rispetto alle precedenti e immaginiamo di trasporla attraverso un “dizionario di colori” che:
- traduca in “rosso” il colore che, nella nuova soluzione, è stato usato per la casella all’incrocio della prima riga con la prima colonna;
- traduca in “verde” il colore che, nella nuova soluzione, è stato usato per la casella all’incrocio della seconda riga con la prima colonna;
- traduca in “giallo” il colore che, nella nuova soluzione, è stato usato per la casella all’incrocio della terza riga con la prima colonna;
- traduca in “porpora” il colore che, nella nuova soluzione, è stato usato per la casella all’incrocio della quarta riga con la prima colonna;
- traduca in “azzurro” il colore che, nella nuova soluzione, è stato usato per la casella all’incrocio della quinta riga con la prima colonna.
Operata questa traduzione, avremo sicuramente ottenuto una delle due soluzioni date qui sopra. Non c’è motivo per far confrontare ai ragazzi le loro soluzioni con quelle proposte qui sul sito, ma potrebbe invece essere utilissimo far loro confrontare le soluzioni proposte dai diversi gruppi interni alla classe: cercare quali tra le loro soluzioni sono effettivamente diverse e quali invece sono uguali (a meno di opportune e oneste traduzioni dei colori) e far loro scoprire che quelle effettivamente diverse sono due soltanto può essere un modo per lavorare sull’uguaglianza in maniera significativa.
Un problema difficile
Come Arthur Conan Doyle fa dire a Sherlock Holmes in I pupazzi ballerini, “Ogni problema diventa di una semplicità infantile appena ci viene spiegato”! E questo rende sempre… difficile… valutare il grado di difficoltà di un problema. Al di là dei giochi di parole, il testo che qui abbiamo scelto di dare può essere adatto (sia perché non richiede alcun prerequisito sia perché è sufficientemente sfidante) anche per bambini dei primi anni della scuola primaria.
Man mano che i ragazzi crescono, “Il patchwork quadrato” può rimanere un problema significativo (e non diventare un puro passatempo) se si aumenta pian piano il grado di difficoltà, dando spazio ad alcune domande che potrebbero nascere dai ragazzi stessi o che l’insegnante potrebbe aggiungere al testo: ne diamo alcuni esempi nel paragrafo seguente.
Un problema aperto
Tra le domande che potrebbero sorgere dal confronto delle soluzioni trovate da diversi gruppi di ragazzini, ve ne sono alcune che riguardano il contare quante sono le soluzioni possibili:
- Scelti i cinque colori e scelto un modo per disporli sulla prima colonna, quante soluzioni diverse al problema si possono trovare?
- Scelti i cinque colori, ma senza imporre un particolare ordine sulla prima colonna, quante soluzioni diverse al problema si possono trovare?
Un’altra strada che “Il patchwork quadrato” ci invita a percorrere è quella verso l’argomentazione:
- In che modo potreste convincere un vostro amico scettico del fatto che, fissati i colori sulla prima colonna, le soluzioni al problema sono soltanto due?
- In che modo potreste convincere un vostro amico scettico del fatto che, con 16 riquadri di stoffa (4 per ciascun colore) il problema non ammette soluzione?
- In che modo potreste convincere un vostro amico scettico del fatto che con 9 riquadri di stoffa (3 per ciascun colore) il problema non ammette soluzione?
- Riuscite ad argomentare questi fatti senza analizzare caso per caso, ma con un ragionamento che vi eviti di provare tutte le possibili configurazioni?
Un problema di matematica con effetto sorpresa
Per i ragazzi può essere sorprendente dover affrontare un problema di matematica “senza numeri”. A dire il vero, nel testo qualche numero compare: si sa che i riquadri sono 25, di 5 colori diversi, 5 per ciascun colore.
Ma, diversamente da come capita spesso di fronte ai problemi classicamente presenti sui libri di testo, qui non si tratta di trovare l’operazione (o le operazioni) da fare con questi numeri; tanto più che, fornendo direttamente i riquadri di stoffa (o di carta), questi dati si potrebbero tranquillamente omettere.
Accanto a questa sorpresa, può essercene un’altra di segno opposto: i numeri possono diventare delle etichette comode per indicare i colori, come nelle figure qui sotto.
È possibile che gli alunni scelgano anche delle altre “etichette” per fare i loro tentativi (R al posto del colore rosso, V al posto del verde, G per giallo, P per porpora e A per azzurro, ad esempio).
Un’altra sorpresa, sulla quale si può fare leva per approfondire la questione, è la simmetria della soluzione. L’approccio che più spesso i ragazzi hanno è quello di disporre i cinque colori sulla prima riga (o sulla prima colonna) e poi proseguire per tentativi, escludendo quelli che portano due riquadri dello stesso colore a toccarsi. È solo a giochi fatti, spesso, che i ragazzi si accorgono di alcune regolarità che inizialmente non si aspettavano.
Per entrambe le soluzioni, accade che in ogni colonna (e in ogni riga) i colori compaiono sempre nello stesso ordine.
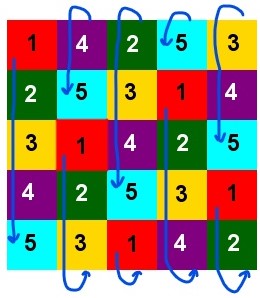
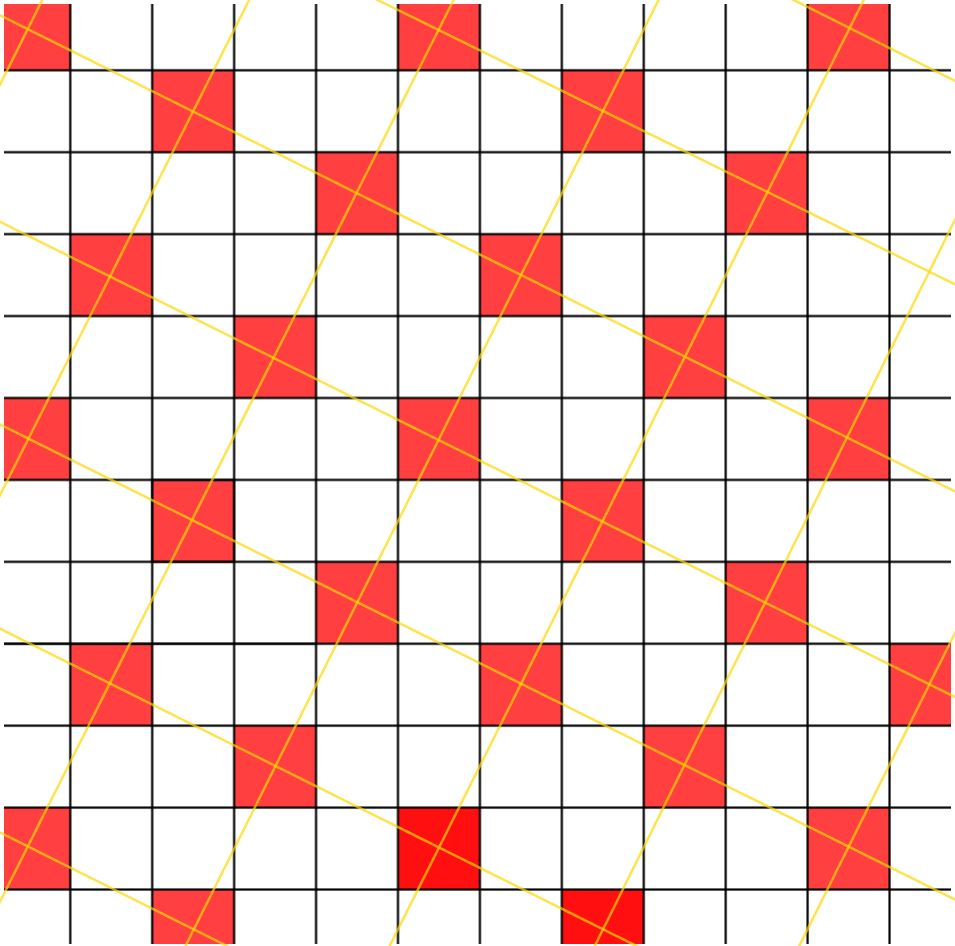
Immaginando di ripetere all’infinito il disegno ottenuto, se facendo un certo percorso si va da un riquadro di un colore ad un altro riquadro dello stesso colore (nel nostro caso: spostandosi per esempio di due caselle in su e di una casella verso destra), allora partendo da un riquadro qualsiasi e facendo lo stesso “percorso” si arriverà a un riquadro dello stesso colore di quello di partenza.
Sempre immaginando di ripetere all’infinito il disegno ottenuto, può essere interessante guardare globalmente la disposizione di un colore soltanto. Ci si accorge che i quadrati rossi (per esempio, ma la stessa cosa vale anche per ogni altro colore) sono disposti in maniera tale che i loro centri sono vertici di una tassellazione in quadrati.
Un problema memorabile
“Il patchwork quadrato”, per la nostra esperienza, è uno di quei problemi che difficilmente si dimenticano, tanta è la sorpresa che suscitano.
Una caratteristica che può renderlo ancora più memorabile, se ce ne fosse bisogno, è il fatto che si tratta di un problema tutt’altro che “scolastico”, tant’è vero che ha richiamato l’interesse di artisti che con la scuola non hanno particolarmente a che fare. Per esempio, alcune opere del grafico svizzero Richard Paul Lohse (1902-1988) sembrano proprio essere la soluzione al problema uguale al nostro, ma con 6×6 riquadri.
Si tratta inoltre di un problema “antico”: le soluzioni al nostro problema, infatti, sono “quadrati latini” con una condizione in più (non può esserci lo stesso numero nemmeno in due caselle che si toccano per un vertice). Un quadrato latino nxn è una griglia quadrata di n2 caselle in ciascuna delle quali compare un simbolo (scelto tra n simboli diversi) in modo tale che in ogni riga e in ogni colonna ciascun simbolo compaia una volta sola. (Per inciso, anche le soluzioni ai Sudoku sono quadrati latini con una condizione in più…)
Anche se i matematici iniziarono più tardi a studiarli, l’origine dei quadrati latini risale almeno ai dintorni dell’anno 1000: le comunità arabe e indiane li usavano, insieme ai quadrati magici, come amuleti o talismani.
Scenari possibili
“Il patchwork quadrato” si presta ad essere proposto a qualsisi età, ovviamente scegliendo opportunamente le domande da porre a contorno del problema principale. Ai bambini più piccoli si potranno dare in mano cartoncini colorati e spiegare la richiesta oralmente o con alcuni esempi, magari arricchendo la narrazione di alcuni particolari sulla coperta della nonna di Alessandra. Ai ragazzi più grandi, invece, si potrà chiedere di rappresentare graficamente i propri tentativi e, soprattutto, di trovare delle argomentazioni valide rispetto al numero delle soluzioni esistenti.
Materiale necessario
Chiaramente i ragazzi possono fare dei tentativi “su carta”, colorando i quadretti del quaderno o associando ad ogni colore un simbolo e scrivendo sulla carta questi simboli.
Consigliamo però di fornire agli alunni dei quadrati di carta colorata che possano davvero essere messi in un certo ordine, staccati e riposizionati fino a che i ragazzini avranno trovato una disposizione opportuna (i foglietti adesivi per appunti possono andare benissimo a questo scopo).
Problema tratto da…
Come spesso accade, anche nel caso de “Il patchwork quadrato” non è possibile risalire a chi ha inventato questo problema, a chi se l’è posto per primo o a chi per primo l’ha proposto ai propri alunni. A noi l’ha fatto tornare in mente Alessandra Gamba, che a lungo ha lavorato come maestra e che è ora impegnata nella formazione degli insegnanti, anche nei corsi MathUp.


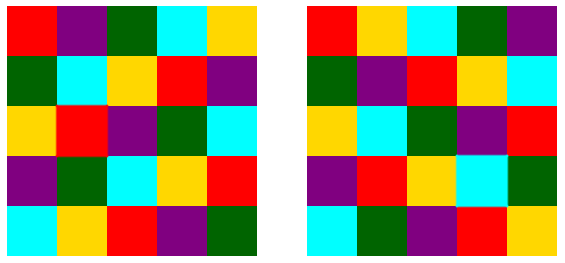




Fantastico!
Hai ragione: noi abbiamo fatto del nostro meglio per commentarlo come si deve, ma quello che è certo è che questo problema, di per sè, è davvero fantastico!