Questo è un problema che potreste esplorare anche a occhi chiusi, cercando di esercitare la vostra fantasia, e discutendo fra di voi in modo da usare l’immaginazione di tutti. Pensiamo però che a un certo punto vi sarà utile aprire gli occhi e provare a costruire qualche oggetto.
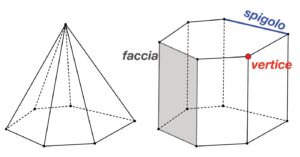
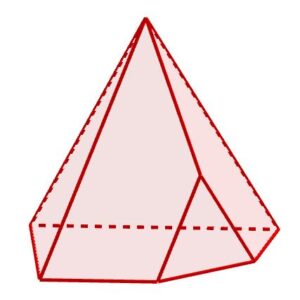
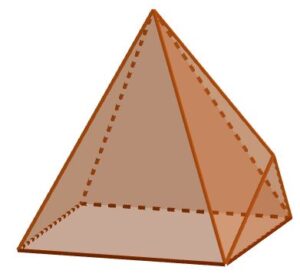
Per fissare le idee sui nomi, in figura vedete una piramide (a sinistra) e un prisma (a destra). Nel prisma abbiamo poi messo in evidenza un vertice (in rosso), uno spigolo (in blu) e una faccia (in grigio).
Sapreste allora immaginare, oppure costruire:
- una piramide con 5 facce? un prisma con 5 facce?
- una piramide con 9 vertici? un prisma con 9 vertici? una piramide con 15 spigoli? un prisma con 15 spigoli?
- un poliedro che abbia lo stesso numero di facce e di vertici?
- un poliedro con 20 spigoli? un poliedro con 21 spigoli? uno con 12 spigoli? uno con 99 spigoli? uno con 100 spigoli? uno con 11 spigoli?
- un poliedro con 6 facce, tutte triangolari? un poliedro con 11 facce, tutte triangolari? un poliedro con 12 facce, tutte triangolari?
Attenzione: alcune di queste richieste (per l’esattezza, tre) sono impossibili. Vi chiediamo allora:
- di descrivere (per iscritto) i poliedri che avete immaginato (o che avete costruito), come se doveste far capire di che si tratta a un vostro amico che non li vede;
- di dire quali sono le tre richieste impossibili da soddisfare. Magari sapete anche spiegare perché sono impossibili?
Soluzione
- Una piramide a base quadrangolare ha 5 facce.
Un prisma a base triangolare ha 5 facce. - Una piramide a base ottagonale ha 9 vertici.
Non esiste un prisma con 9 vertici, perché i vertici dei prismi sono sempre in numero pari, il doppio dei vertici del poligono di base.
Non esiste una piramide con 15 spigoli, perché gli spigoli delle piramidi sono sempre in numero pari, il doppio dei lati del poligono di base.
Un prisma a base pentagonale ha 15 spigoli. - Ogni piramide ha lo stesso numero di facce e di vertici.
- Una piramide a base decagonale è un esempio di poliedro con 20 spigoli.
Un prisma a base ettagonale è un esempio di poliedro con 21 spigoli.
Un prisma a base quadrangolare è un esempio di poliedro con 12 spigoli; anche una piramide a base esagonale è un esempio di poliedro con 12 spigoli.
Una piramide che ha per base un poligono di 50 lati è un esempio di poliedro con 100 spigoli.
Un prisma che ha per base un poligono di 33 lati è un esempio di poliedro con 99 spigoli.
(Quelli qui citati sono solo esempi, ma se ne possono trovare anche altri al di fuori di prismi e di piramidi.)
Un poliedro con 11 spigoli si può ottenere (ad esempio) da una piramide a base quadrangolare, tagliandone via una piccola piramide (a base triangolare) vicino a un vertice. Così come si può ottenere (tanto per fare un altro esempio) appiccicando una piramide a una delle facce triangolari di una piramide quadrangolare. - Una bipiramide ottenuta incollando le basi di due piramidi a base triangolare è un esempio di poliedro con 6 facce, tutte triangolari.
Una bipiramide ottenuta analogamente a partire da due piramidi a base esagonale è un esempio di poliedro con 12 facce, tutte triangolari.
Non esiste un poliedro con 11 facce, tutte triangolari; infatti, immaginiamo di avere a disposizione 11 triangoli, che dovrebbero diventare le 11 facce del poliedro; in totale, i lati a nostra disposizione sono 11×3=33; nel costruire il poliedro, ciascuno di questi lati dovrebbe andare a combaciare con un altro lato (di un altro triangolo), per diventare uno spigolo del poliedro; ma allora è chiaro che non riusciremo mai a chiudere un poliedro usando tutti (e soli) questi triangoli, perché 33 è un numero dispari.
Commenti
Un problema significativo
Ciò che rende particolarmente interessante questo problema è il fatto che esso fa da ponte tra tanti ambiti della matematica, spesso considerati lontani, o quanto meno separati, nella scuola del primo ciclo: la geometria e l’aritmetica in primo luogo, ma anche l’algebra e la topologia…
Un ponte tra geometria e aritmetica
Ragionando su questo problema (e magari costruendo anche alcuni degli oggetti in esso coinvolti) gli alunni si possono accorgere di alcuni fatti:
- il numero dei vertici di un prisma è sempre il doppio del numero dei vertici del poligono di base;
- il numero degli spigoli di una piramide è sempre il doppio del numero dei vertici del poligono di base;
- il numero degli spigoli di un prisma è sempre il triplo del numero dei lati del poligono di base.
Capita però che (anche tra ragazzini di terza media), alla richiesta di descrivere un prisma con 9 vertici, qualcuno risponda dicendo che si tratta di un prisma con il poligono di base di 4,5 vertici; come c’è chi (probabilmente rendendosi conto che il numero 4,5 non può descrivere quanti vertici ha un poligono), conclude che il perimetro (o il lato) del poligono di base del prisma deve essere lungo 4,5 cm…
Si tratta di errori che, solitamente, vengono presto riconosciuti come tali, e che danno l’occasione ai ragazzi di riflettere sulle caratteristiche e le differenze tra i diversi tipi di numeri che hanno incontrato; in particolare questo problema aiuta a mettere in luce il fatto che in risposta ad alcune domande (le domande che prevedono un contare) ci aspettiamo a priori numeri di un certo tipo (naturali) e non di un altro. Come a dire: il numero dei vertici di un prisma è sempre un numero naturale ed è sempre pari, perché è il doppio del numero dei vertici del poligono di base, che è anch’esso un numero naturale. La stessa cosa vale per il numero degli spigoli della piramide. E il numero degli spigoli di un prisma è sempre un numero naturale ed è un multiplo di tre, perché è il triplo del numero dei lati del poligono di base, che è anch’esso un numero naturale.
Un ponte tra geometria e algebra
Per risolvere questo problema, in particolar modo per giustificare il fatto che non esiste un prisma con 9 vertici né una piramide con 15 spigoli, gli alunni devono accorgersi della relazione che esiste tra il numero dei lati della base di un prisma (o di una piramide) e quello dei suoi vertici (o dei suoi spigoli). Pur non essendo esplicitamente richiesto che i ragazzi esprimano queste relazioni con delle espressioni letterali, accade che, in classi che hanno una certa confidenza con l’uso delle lettere al posto dei numeri, gli alunni al termine di questo problema riconoscano che:
- un prisma che abbia per base un poligono con n lati ha 2n vertici, 3n spigoli e n+2 facce;
- una piramide che abbia per base un poligono con n lati ha n+1 vertici, 2n spigoli e n+1 facce.
Se la familiarità della classe con le espressioni letterali non è ancora tale da far venire in mente agli studenti di scrivere queste relazioni in questo modo, può essere l’insegnante a richiederlo: sarà per tutti un buon esempio di un uso significativo delle lettere al posto dei numeri.
Un ponte tra geometria e topologia
Chiedere agli alunni che trovino le relazioni tra il numero dei lati della base di un prisma (o di una piramide) e il numero dei suoi vertici, delle sue facce e dei suoi spigoli può essere un buon modo per verificare se essi hanno capito come è fatto un prisma (o come è fatta una piramide). Può anche essere una situazione semplice in cui far esercitare i ragazzi nell’uso di espressioni letterali (che siano cariche di significato e non solo simboli da manipolare).
Ma c’è di più: soffermarsi con i ragazzi sul numero di vertici, facce e spigoli di questi poliedri, significa incominciare a dare importanza a questi numeri e, piano piano, alla struttura combinatoria dei poliedri.
Tanto per fare un esempio, per giustificare l’impossibilità di un poliedro con 11 facce, tutte triangolari, i ragazzi devono capire a fondo i nessi fra tutti i numeri coinvolti, il numero F delle facce, il numero dei lati di ogni faccia, il numero S degli spigoli del poliedro che si andrà a formare; e rendersi conto quindi che, se tutte le facce hanno 3 lati, dovrà valere una relazione del tipo 3F=2S. E, probabilmente, chi è arrivato a farsi una ragione della impossibilità di un poliedro con 11 facce triangolari è “passato vicino” a questa relazione, anche se naturalmente non ci aspettiamo che arrivi spontaneamente dai ragazzi una scrittura di questo genere.
A partire da questo problema, o da altri analoghi, si può iniziare a lanciare qualche sguardo in un mondo particolarmente profondo, quello della topologia: a seconda dell’interesse mostrato dai ragazzi e dall’ordine di scuola in cui si trova, l’insegnante potrà decidere se spingersi fino a presentare la relazione di Eulero, o se addirittura porre il problema dell’ambito della sua validità [1].
Un problema difficile
Nel complesso “Prismi, piramidi e altro” non è un problema troppo difficile, o meglio: le classi in cui è stato proposto non l’hanno trovato più difficile di tanti altri Problemi per matematici in erba!
Ci sono però alcune richieste che possono dare del filo da torcere non solo agli alunni della secondaria di primo grado, ma anche a quelli della scuola superiore.
Il “salto” di difficoltà si ha laddove gli alunni devono riconoscere alcune richieste impossibili da soddisfare: convincersi (e convincere i propri interlocutori) del fatto che una piramide a base esagonale ha 12 spigoli è decisamente più facile rispetto al convincersi (e al convincere) del fatto che una piramide con 15 spigoli non esiste!
Qual è il motivo di questa maggiore difficoltà?
Innanzitutto, prima ancora di cercare di capire quale delle richieste è impossibile, bisogna accettare (e comprendere) il fatto che non basta poter parlare (o scrivere) di qualcosa, perché questa cosa esista. Quando parlo di un “prisma con 9 vertici” non risulta immediatamente evidente una contraddizione; la contraddizione emerge solo se vado a considerare tanti fatti interconnessi: la definizione di prisma, la relazione che c’è tra il numero dei vertici della base del prisma e il numero totale dei suoi vertici, il fatto che questi numeri debbano essere entrambi interi, il fatto che il doppio di un numero intero debba essere per forza pari… In generale, ogni volta che dobbiamo dimostrare che un certo oggetto matematico non esiste, dobbiamo fare riferimento a una contraddizione che può emergere solo facendo un passo indietro e andando a verificare le tante condizioni che quell’oggetto dovrebbe soddisfare.
Dimostrare che qualcosa è impossibile richiede quindi una comprensione profonda del contesto nel quale ci si sta muovendo; in altre parole richiede una consapevolezza delle “regole” di questo contesto decisamente maggiore di quella necessaria solo per costruire oggetti che obbediscano a quelle regole. Quando parliamo di un poliedro con 11 facce, tutte triangolari, non è immediatamente evidente una contraddizione, come si diceva sopra. Essa emerge solo se gli alunni hanno acquisito (o acquisiscono nel momento in cui risolvono questo problema) consapevolezza di una regola che hanno applicato ogni volta che hanno costruito un poliedro: ogni spigolo è comune a esattamente due facce. Si tratta di una regola così basilare che nemmeno ci si pensa, quando la si applica per costruire un poliedro: viene naturale unire una faccia all’altra per uno spigolo, senza lasciare buchi e senza incernierare più di due facce alla volta. Ma proprio perché è una regola così basilare finisce che non ci si pensa, almeno non fino a quando non si è costretti a farlo, come lo si è da questa richiesta… impossibile!
Sperimentazione e possibili scenari
Nell’anno scolastico 2017 / 2018 abbiamo potuto osservare le soluzioni di questo problema proposte dagli alunni di cinquantaquattro classi terze della scuola secondaria di primo grado.
In moltissimi casi, prima di assegnare il problema, l’insegnante aveva avuto cura di fare in modo che la classe prendesse confidenza con i prismi e le piramidi, facendo costruire modellini di cartoncino, di polydron [2], con i geomag [3], ma anche con cannucce e nettapipe, stecchini di varie lunghezze, plastilina… In alcuni casi, invece di far costruire ai ragazzi una ampia varietà di solidi, si sono forniti loro alcuni modelli, contenuti in kit in dotazione alla scuola. È emerso che avere pochi modelli (in genere nei kit commercializzati sono presenti un cubo, un parallelepipedo, un prisma con la base non quadrangolare, una piramide a base quadrata, un cono, un cilindro e una sfera) ha limitato la capacità di immaginazione dei ragazzi, che sono rimasti legati a quella piramide e a quel prisma, invece di sentirsi liberi di pensarne di diversi.
Una nota positiva emersa in tutte le classi in cui questo problema è stato sperimentato riguarda l’atteggiamento di ricerca che, da subito, ha favorito nei ragazzi: l’invito a cimentarsi con la costruzione dei solidi e il sapere che alcune delle richieste erano impossibili hanno tenuto alta la motivazione e spinto nella ricerca anche coloro che tenderebbero a cercare tutte le risposte nella propria memoria o a ricavarle da qualche formula.
La difficoltà più grossa è stata motivare l’impossibilità di soddisfare le tre richieste impossibili, il che era del tutto prevedibile e previsto (non a caso, la domanda in questione è stata fatta precedere da un “Magari…”!). Questa domanda, presentata qui in qualche modo come “facoltativa”, potrebbe invece diventare il nocciolo dello stesso problema se lo si volesse presentare nelle classi prime o seconde della scuola secondaria di secondo grado. In quest’ordine di scuola si potrebbe anche esplicitare la richiesta di esprimere il numero delle facce, degli spigoli e dei vertici di una piramide e di un prisma in funzione del numero n dei lati della loro base.
Ci immaginiamo che “Prismi, piramidi e altro” possa essere proposto con successo anche in nella scuola primaria, se ai bambini viene prima (o contestualmente) data la possibilità di osservare e costruire tanti prismi, tante piramidi e tanti altri poliedri, in tanti modi diversi.
Materiale necessario
“Prismi, piramidi e altro” si apre con la dichiarazione che il problema potrebbe essere esplorato anche a occhi chiusi. È vero; anzi: riuscire a immaginare i poliedri senza averne tra le mani un modello è uno degli scopi del nostro insegnamento della geometria. È però vero anche che questa capacità di immaginarsi gli oggetti tridimensionali nasce dall’averne guardati, toccati e costruiti di reali. Così come è vero, anche se a prima vista potrebbe sembrare di avere a che fare con un gatto che si morde la coda, che per costruire un prisma, una piramide o un poliedro con certe caratteristiche dobbiamo prima essercelo immaginato!
In altre parole: il passaggio dal concreto all’astratto non avviene una volta per tutte, in un solo momento. E quindi, qualsiasi età abbiano gli alunni ai quali proponiamo questo problema, è bene che essi abbiano la possibilità di alternare momenti in cui costruiscono, osservano e manipolano a momenti in cui immaginano, guardano e toccano con occhi e mani che sono “solo” mentali.
Più (e più diversi tra loro) sono i modelli che i ragazzi potranno osservare e costruire, maggiore sarà la possibilità che essi distinguano le caratteristiche valide per tutte le piramidi (o per tutti i prismi) da quelle valide, tanto per fare un esempio, solo per le piramidi rette a base quadrata (o solo per i prismi retti a base esagonale).
Più sono vari i materiali a disposizione dei ragazzi, maggiore sarà la probabilità che essi non confondano le proprietà di un certo materiale e dei modelli che con quel materiale sono stati costruiti, con le proprietà dei poliedri che quei modelli rappresentano.
Tra i materiali utilizzabili ricordiamo:
- polydron [2];
- geomag [3];
- cartoncino (sul sito di Gijs Korthals Altes si trovano moltissimi modelli di poliedri, scaricabili per essere stampati, ritagliati, piegati e incollati);
- stecchini di legno (stuzzicadenti, spiedini…) e pasta per modellare;
- scatole diverse recuperate dalle case nostre e dei nostri alunni;
- cannucce e nettapipe…
Strumenti digitali
Nel caso non sia possibile far costruire e manipolare agli alunni oggetti concreti a forma di piramidi, prismi e altri poliedri, sarà utile mostrare ai ragazzi tanti “oggetti virtuali”, piuttosto che solo i (solitamente pochi e stereotipati) disegni presenti sui libri di testo. A tal fine può essere utile l’uso di GeoGebra3D, come mostrato nei video seguenti, che sono stati pensati in particolar modo per quelle classi che dovranno affrontare lo studio di prismi e piramidi “a distanza”.
Il primo video può essere utilizzato per far osservare, ad alunni che abbiano già chiaro che cosa sono prismi e piramidi, quanti sono i vertici, gli spigoli e le facce degli uni e delle altre.
Il secondo e il terzo video, anch’essi pensati per classi che si trovano a dover lavorare solo o prevalentemente attraverso la didattica digitale, possono aiutare gli alunni a trovare una definizione condivisa di prisma e di piramide.
Problema tratto da…
Questo problema è stato proposto tra quelli della sperimentazione legata al corso MathUp per la classe terza della Scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.
Prismi, piramidi e altro, inoltre, è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020) un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.
Note
[1] Detto V il numero dei vertici di un poliedro, S il numero dei suoi spigoli e F il numero delle sue facce, per tutti i poliedri semplicemente connessi si ha che
V-S+F=2.
I poliedri semplicemente connessi, per intenderci, sono quelli che – se li immaginiamo con le facce di gomma e gonfiabili – si possono deformare in una sfera. Se un poliedro ha “un buco”, ossia se possiamo immaginarci di gonfiarlo fino a farlo diventare un salvagente, la somma V-S+F non vale più due, ma zero. Si dice anche che i poliedri deformabili in una ciambella hanno caratteristica di Eulero uguale a zero.
[2] Si tratta di uno strumento, come altri esistenti in commercio, che consiste di tessere poligonali di diverse forme, con la possibilità di incastrarle fra loro.
[3] Si tratta di un giocattolo di costruzione magnetica, come altri esistenti in commercio, che permette di realizzare anche diversi poliedri.