La storia
L’altro giorno Chiara discuteva con due suoi amici; erano presenti anche Alberto, il cugino grande di Chiara, che studia ingegneria all’università, e sua zia, che fa la ricercatrice in matematica. Chiara è ancora alla scuola primaria, ed è una ragazzina sveglia a cui piace giocare con i numeri; prima ha detto ai suoi amici che lei (da vera maghetta) sa che 9x9x9x9x9 è un numero che finisce per 9; e fin qui tutti le han creduto, anche perché lo hanno verificato con la calcolatrice. Ma poi li ha addirittura sfidati in questo modo: Voi ditemi un numero, qualsiasi, anche grandissimo, e io vi so dire qual è l’ultima cifra di 9x9x… moltiplicando tanti 9 quanti ne indica il numero che mi avete detto. E se non è magia questa…!
Chiara non ha ancora studiato le potenze e non sa usare bene le lettere al posto dei numeri; noi avremmo potuto anche dire così: Voi ditemi un numero qualsiasi n e io vi so dire qual è l’ultima cifra di 9n.
A suo cugino Alberto questa sembra una spacconata inverosimile (anche perché, quando il numero diventa davvero grande, non si riesce a verificarlo nemmeno con la calcolatrice…!); però la zia ha detto che Chiara ha ragione, che si può fare, in maniera abbastanza semplice, e che si potrebbe fare anche con altri numeri al posto del 9; ha aggiunto addirittura che la calcolatrice per questo problema non serve proprio a niente.
E voi? Avete capito qual è il “trucco” di Chiara? E perché questo trucco funziona?
Le domande
Qual è l’ultima cifra di 97? e di 94? e di 957? e di 92018? e di 92019?
Il cugino di Chiara non ha capito come funziona e Chiara glielo deve spiegare. Aiutatela:
- se l’esponente è … allora 9 elevato a quell’esponente finisce per …
- se invece l’esponente è … allora 9 elevato a quell’esponente finisce per …
Il cugino di Chiara è proprio testardo. Nonostante Chiara gli abbia svelato il suo “trucco”, quasi si arrabbia: Non ci credo! Nei casi che riesco a controllare facendo i conti con la calcolatrice è vero, va bene, ma questo non ci assicura per niente che poi la stessa cosa sia vera sempre! Come fareste a convincerlo che invece è proprio così?
E ora provate a giocare con qualche altro numero.
Se Chiara, invece del 9, avesse usato il 5, il problema sarebbe stato più facile. Qual è l’ultima cifra di 52018? e di 52019? Sapreste formulare una regola generale sull’ultima cifra di una (qualsiasi!) potenza di 5? Come scrivereste questa regola? Perché siete sicuri che funziona sempre?
Sapreste trovare un altro numero che si comporta come il 5, per cui il gioco di Chiara è molto facile? Quale? E perché anche con questo numero succede lo stesso fenomeno che succede col 5?
Ecco invece un caso più complicato.
Qual è l’ultima cifra di 72? e di 73? e di 74? e di 75? e di 757? e di 72018? e di 72019?
Per indovinare qual è l’ultima cifra di 7 elevato a un numero qualsiasi basta guardare l’esponente. Ma quale caratteristica dell’esponente occorre guardare?
Alberto continua a dire che non ci crede. Come fate a convincerlo che le cose stanno proprio come dice Chiara?
Soluzione
Per le potenze di 9:
- se l’esponente n è un numero pari, l’ultima cifra di 9n è 1;
- se l’esponente n è un numero dispari, l’ultima cifra di 9n è 9.
Per le potenze di 5:
- l’ultima cifra di 5n è sempre 5, qualunque sia n (n>0). Gli altri numeri (fra 0 e 9) che si comportano come il 5 sono 6, 0, 1.
Per le potenze di 7:
- se l’esponente n è un multiplo di 4, allora 7n finisce per 1; in particolare 74 finisce per 1;
- se l’esponente n è un numero che diviso per 4 dà resto 1, allora 7n finisce per 7; in particolare 75 e 757 finiscono per 7;
- se l’esponente n è un numero che diviso per 4 dà resto 2, allora 7n finisce per 9; in particolare 72 e 72018 finiscono per 9;
- se l’esponente n è un numero che diviso per 4 dà resto 3, allora 7n finisce per 3; in particolare 73 e 72019 finiscono per 3.
Commenti
Lo scopo della lunga storiella è proprio quello di insistere con i ragazzi sull’importanza delle informazioni che si possono leggere “fra le righe” di un testo. Alcune informazioni che si possono discutere con loro per verificare se le hanno colte dal testo sono:
- il problema non richiede conoscenze particolari, è accessibile a una ragazzina (sveglia) di scuola primaria, con la quale gli alunni più piccoli potrebbero identificarsi;
- nonostante questo, è un problema difficile (mette in crisi Alberto, che studia all’università);
- la zia matematica (e quindi affidabile, perlomeno per questo problema…!) conferma che una buona idea, che può venire anche a una ragazzina di scuola primaria, può risolvere il problema; e che non servono conti difficili né tantomeno la calcolatrice.
Accanto all’analisi e all’interpretazione del testo, l’altro nodo importante di questo problema sta nella argomentazione. L’osservazione cruciale, che motiva poi tutti i risultati qui sopra, è il fatto che la cifra delle unità del prodotto di due numeri naturali dipende esclusivamente dalla cifra delle unità dei due fattori. Quindi, per esempio, per quel che riguarda le potenze di 9, essendo 9x9=81, anche il prodotto di due numeri qualsiasi che terminano con la cifra 9 terminerà sempre con la cifra 1; e, essendo 1x9=9, anche il prodotto di due numeri che terminano uno con la cifra 1 e l’altro con la cifra 9 terminerà sempre con la cifra 9. Si può osservare anche che la stessa “osservazione cruciale” ci garantisce che ciò che abbiamo detto per il 9 vale anche per un qualsiasi numero che finisce per 9: ogni sua potenza a esponente pari termina con la cifra 1 e ogni sua potenza a esponente dispari termina con la cifra 9. Quindi, se Chiara vuole continuare a fare la maghetta può sbizzarrirsi e vantarsi di essere capace anche di trovare la cifra finale di un’arbitraria potenza di 79 o di 2019.
Analogo, ma ancora più semplice è il discorso con le potenze di 5: infatti, essendo 5x5=25, anche il prodotto di due numeri che terminano con la cifra 5 terminerà sempre con la cifra 5, e quindi in particolare tutte le potenze di 5 terminano con la cifra 5; e la stessa cosa vale anche per tutte le potenze di 75, o di 425, o di un qualsiasi numero che finisce per 5. Un analogo discorso vale per il 6 (dato che 6x6=36) e anche per i due casi un po’ “strani”, cioè lo 0 e l’1. Qui sembra che non ci sia niente da dire perché, dato che 0x0=0 e 1x1=1, sappiamo anche subito che tutte le potenze di 0 sono uguali a 0 e tutte le potenze di 1 sono uguali a 1, e quindi è anche superfluo parlare di ultima cifra. Però, come prima, possiamo aggiungere che anche un’arbitraria potenza di un qualsiasi numero che finisce per 0 ha cifra finale 0; così come un’arbitraria potenza di un qualsiasi numero che finisce per 1 ha cifra finale 1.
Il discorso è un po’ più complicato per quel che riguarda il 7, ma l’idea sottostante è la stessa: dato che 7x7=49, sappiamo che anche il prodotto di due numeri che terminano con la cifra 7 terminerà sempre con la cifra 9 (in particolare 72 finisce per 9); dato che 9x7=63, sappiamo anche che il prodotto di due numeri che terminano uno con la cifra 9 e l’altro con la cifra 7 terminerà sempre con la cifra 3 (in particolare 73 finisce per 3); dato che 3x7=21, sappiamo anche che il prodotto di due numeri che terminano uno con la cifra 3 e l’altro con la cifra 7 terminerà sempre con la cifra 1 (e in particolare 74 finisce per 1). A questo punto il ciclo si ripete perché, dal fatto che 1x7=7, sappiamo che il prodotto di due numeri che terminano uno con la cifra 1 e l’altro con la cifra 7 terminerà sempre con la cifra 7: in particolare 75 finisce per 7, e poi, per calcolare l’ultima cifra di 76 e delle potenze successive, possiamo usare le osservazioni già fatte. Resta allora solo da osservare che il ciclo si ripete ogni 4 e quindi la cifra finale sarà 7, 9, 3, 1 a seconda del resto nella divisione per 4 dell’esponente, ovvero l’ultima cifra di 7n è:
- 7, se n = 4m + 1 è un numero che diviso per 4 dà resto 1;
- 9, se n = 4m + 2 è un numero che diviso per 4 dà resto 2;
- 3, se n = 4m + 3 è un numero che diviso per 4 dà resto 3;
- 1, se n = 4m è un multiplo di 4.
Anche in questo caso, lo stesso risultato vale non solo per le potenze del numero 7, ma anche per le potenze di un qualsiasi numero che termina con la cifra 7.
Mediamente è probabile che i ragazzi non abbiano eccessive difficoltà a scoprire come si alternano le cifre finali delle potenze di 9, né tanto meno il fatto che le potenze di 5 finiscono sempre per 5. Per ipotizzare una regola generale a proposito dell’ultima cifra delle potenze di 7, ci aspettiamo che i ragazzi abbiano l’esigenza di andare un po’ più avanti con tentativi e calcoli. Sarà interessante osservare in che modo organizzano i loro dati. È utile che si rendano conto (direttamente dal loro lavoro, senza che qualcuno glielo dica in astratto) che sistemare ordinatamente i propri risultati può essere il punto significativo che fa scattare la “buona idea” con cui proseguire.
Ancora più complesso, naturalmente, sarà arrivare a dare una sorta di giustificazione di questo fatto. Come ben dice uno degli alunni che hanno già affrontato questo problema:
È così, ma non riesco a spiegare perché!
Per motivare i ragazzi ad argomentare, si può far leva sul desiderio di evitare i conti e di risparmiarsi moltiplicazioni su moltiplicazioni. Non ci aspettiamo certo una motivazione formale, però almeno alcuni ragazzi potrebbero arrivare a scoprire quella che abbiamo chiamato “osservazione cruciale”, ossia il fatto che l’ultima cifra di un prodotto dipende solo dalle ultime cifre dei fattori.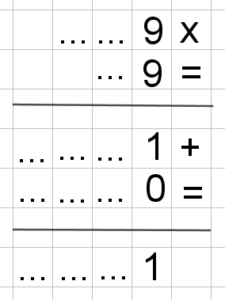
A questa osservazione gli alunni possono giungere prestando attenzione a che cosa succede quando fanno le operazioni in colonna. Ed è anche per questo motivo che la zia di Chiara insiste sul fatto che la calcolatrice non serve: non solo non serve perché, appena i numeri diventano un po’ più grandi (e con le potenze diventano presto molto grandi!), la calcolatrice dà segnale di errore, ma soprattutto perché, se solo schiacciano un tasto e acquisiscono un risultato, è più improbabile che i ragazzi notino quella “osservazione cruciale” che li porta poi a risolvere il problema e a fare i maghetti.
Con i ragazzi più grandi si può anche impostare una verifica algebrica (invece dei puntini): si può scrivere (10k + 1) per indicare un numero che finisce con la cifra 1, (10k + 2) per indicare un numero che finisce con la cifra 2 e così via; e quindi la moltiplicazione tra due numeri che terminano con la cifra 9 si scrive così:
(10k+9) x (10p + 9) =
= 100kp + 90p + 90k + 81 =
= 100kp + 90p + 90k + 80 + 1 =
= 10 x (10kp + 9p + 9k + 8) + 1.
Il prodotto è quindi un multiplo di 10 a cui viene aggiunto un 1, cioè si tratta di un numero che termina con la cifra 1.
Vale la pena osservare che la verifica formale algebrica è in realtà concettualmente identica alla operazione in colonna “mimata” con i puntini al posto delle cifre diverse dall’ultima.
In modo assolutamente analogo (con l’algebra oppure con la moltiplicazione coi puntini) si può procedere con tutte le altre verifiche. Per esempio:
Merita un discorso a sé il problema di come “scrivere” la soluzione. Mentre è facile dire e scrivere che cosa succede alle potenze di 5 (per un qualsiasi esponente), ed è anche abbastanza facile spiegare che per le potenze di 9 occorre distinguere tra esponente pari e dispari, la scrittura è più difficile nel caso delle potenze di 7, dove l’elemento significativo è il resto dell’esponente nella divisione per 4.
I ragazzi potranno scrivere le risposte in tanti modi diversi. L’esperienza ci insegna che anche nelle classi terze della scuola secondaria di primo grado i ragazzi mediamente non hanno ancora interiorizzato il resto come uno strumento utile ogni volta che si abbia a che fare con fenomeni che si ripetono con una certa periodicità. In ogni caso, che utilizzino o meno il resto, il punto davvero importante è che i ragazzi diano le loro giustificazioni in maniera comprensibile: leggendo ciò che hanno scritto, una persona diversa da loro deve essere in grado di capire quali caratteristiche osservare sul numero n al fine di decidere l’ultima cifra di 7n.
Sperimentazione e possibili scenari
Un problema molto simile a questo è stato sperimentato in 31 classi terze della scuola secondaria di primo grado durante il corso MathUp per la terza classe della scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.
Alcuni insegnanti già lo scorso anno avevano proposto il medesimo problema anche nelle classi prime e seconde della scuola secondaria di primo grado. Per facilitare i ragazzini più giovani (eventualmente anche delle classi quinte della scuola primaria) suggeriamo di modificare una frase del testo. Dove si dice
“Chiara non ha ancora studiato le potenze e non sa usare bene le lettere al posto dei numeri; noi avremmo potuto anche dire così: Voi ditemi un numero qualsiasi n e io vi so dire qual è l’ultima cifra di 9n.”
si potrebbe sostituire con:
“Chiara non ha ancora studiato le potenze; noi avremmo potuto anche dire così: Voi ditemi un numero qualsiasi e io vi so dire qual è l’ultima cifra di 9 elevato a… proprio quel numero che mi avete detto. Per esempio, se le dite 5, Chiara vi dice che l’ultima cifra di 95 è 9.”
Problema tratto da…
Questo problema è tra quelli proposti nella sperimentazione legata al corso MathUp “Problemi e approfondimenti” per la Scuola secondaria di primo grado nell’anno scolastico 2018 / 2019.
L’ultima cifra, inoltre, è tra i Problemi per matematici in erba citati in Diario di bordo (Sofia Sabatti, edizioni mateinitaly, 2020), un testo nel quale alcuni dei problemi presentati in questo sito vengono contestualizzati all’interno di un anno scolastico vissuto da una classe terza della scuola secondaria di primo grado.
Problemi collegati
Il fregio di Halloween è un problema che può essere risolto, come questo, ponendo attenzione esclusivamente al resto di alcune divisioni.
La calcolatrice ha sempre ragione? e I pasticcini sono altri due problemi che possono essere utili per far riflettere gli alunni sulle caratteristiche della divisione in N.


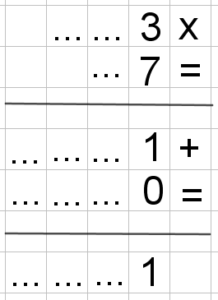
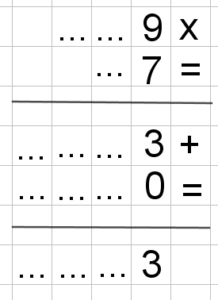
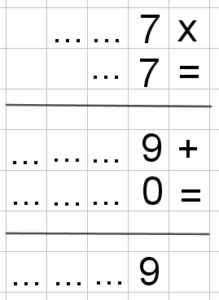


qual’è l’unita di 17 alla diciassettesima
Salve! Scusi, ma non abbiamo capito se ci sta facendo una domanda, o ci sta proponendo un ampliamento per il problema.
Se non ha già letto i commenti nascosti dietro il tasto “mostra tutto”, la invitiamo a farlo: lì dovrebbe trovare gli strumenti che le servono per dare una risposta alla sua questione.
(Non vogliamo eludere la questione… ma non vorremmo servire la risposta su un piatto d’argento a un eventuale studente in cerca di scorciatoie…!)