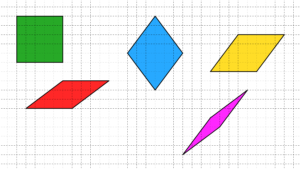
Quanti sono i diversi rombi con il lato di esattamente 5 quadretti che si possono disegnare sulla carta a quadretti in modo che abbiano tutti i vertici negli incroci della quadrettatura?
Un suggerimento: ricordatevi che la diagonale di un rettangolo di lati 3 quadretti e 4 quadretti è lunga esattamente 5 quadretti.
Disegnate, su carta a quadretti, tutti i rombi che avete trovato.
Soluzione
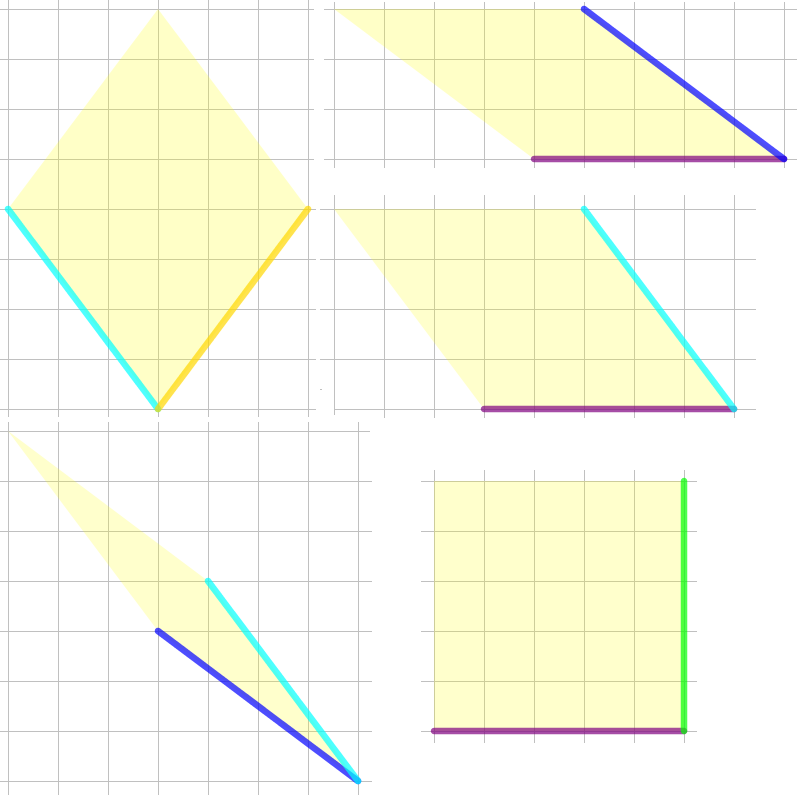
I possibili rombi differenti sono cinque e sono quelli disegnati nella figura qui sotto.
Commenti
Un problema significativo
Il problema sta nel riconoscere, tra i rombi che i ragazzi disegneranno su carta a quadretti, quali sono uguali e quali sono diversi, riflettendo quindi, innanzitutto, su quale possa essere un buon criterio per stabilire se due rombi sono uguali o sono diversi.
Il suggerimento relativo alla diagonale di un rettangolo di lati 3 e 4 quadretti è dato proprio per non distogliere l’attenzione dal cuore del problema: a tutti gli alunni (sia a quelli che abbiano già studiato il teorema di Pitagora, sia a chi non l’avesse ancora affrontato) vengono forniti tutti gli strumenti che possono essere utili per arrivare alla soluzione.
Metacognizione
Un “effetto collaterale” di questo problema potrebbe essere quello di smantellare la convinzione – spesso radicata nei bambini ma anche in ragazzi più grandi – che i rombi siano tali perché hanno le diagonali parallele alle rette della quadrettatura (o, se disegnati su carta bianca, parallele ai bordi del foglio).
Questa convinzione in alcuni ragazzi è talmente forte da impedire di riconoscere un quadrato se i suoi lati non sono paralleli alle linee della quadrettatura…
… e da impedire di riconoscere un rombo, se le sue diagonali non sono parallele alle linee della quadrettatura.
“Rombi sul quaderno a quadretti” forza i ragazzi ad abbandonare questo stereotipo.
Infatti, per decidere se una figura che hanno disegnato è o non è un rombo, e per decidere se due figure tra quelle disegnate sono uguali o diverse, gli alunni che affrontano questo problema non possono fermarsi all’immagine “standard” che hanno visto sui libri di testo: devono, piuttosto, far riferimento alle proprietà che caratterizzano la figura.
Acqusire questa elasticità è una conquista profonda ed essenziale e significa imparare qualcosa di veramente esportabile in altri contesti e in altre situazioni in cui venga richiesto di riconoscere altre figure.
Un problema memorabile
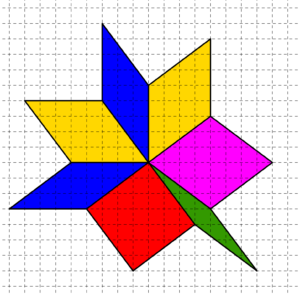
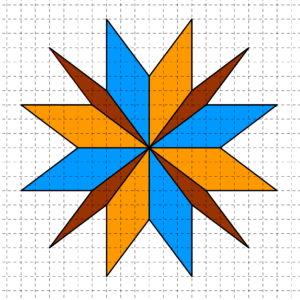
Avremmo potuto contestualizzare “Rombi sul quaderno a quadretti” in un modo molto simile a quello del suo problema “gemello” che, attraverso un testo molto lungo, invita i ragazzi a “studiare” (per poi realizzarne altre) delle ruote fomate da triangoli isosceli con i due lati uguali lunghi 5 quadretti.
Si sarebbe potuta fare una richiesta analoga, riferendosi a “ruote” ottenute accostando rombi di lato cinque quadretti, come per esempio quelle qui sotto.
Abbiamo però deciso di proporre qui un testo molto breve, che va direttamente al cuore “matematico” del problema, senza essere inserito in una storia e senza fare riferimento ad una realtà diversa da quella che caratterizza gli oggetti matematici nella loro astrattezza.
Ogni insegnante potrà, volendo, costruire attorno a questo “nocciolo” una narrazione, rinunciando all’agilità del testo breve, ma potendo così:
- rendere il problema più “memorabile”, più facilmente richiamabile alla mente anche nel futuro;
- creare una motivazione che spinga gli alunni a trovare la soluzione;
- trovare lo spazio per dividere il problema in passi successivi, fornendo alcuni esempi da osservare e su cui ragionare, prima di mettersi a cercarne da soli degli altri;
- dare una buona occasione di interpretazione di un testo.
Un problema aperto
Tante sono le possibili aperture di questo problema verso questioni ad esso legate: ne vogliamo elencare qui solo alcune.
rombi isoperimetrici
I rombi costruiti seguendo la richiesta di questo problema hanno tutti i quattro lati di 5 quadretti, quindi hanno tutti perimetro 20 quadretti.
Come sono le loro aree: uguali o diverse?
Sapreste trovare l’area di tutti i rombi che avete disegnato?
Qual è, tra essi, quello con area maggiore?
Se due rombi hanno sia lo stesso perimetro che la stessa area, sono necessariamente uguali?
E se due quadrilateri qualsiasi (non necessariamente rombi) hanno la stessa area e lo stesso perimetro, sono necessariamente uguali?
argomentazione
Il problema non richiede esplicitamente di argomentare, ma la necessità di spiegare i propri ragionamenti dovrebbe nascere quasi spontaneamente, qualora i ragazzi non fossero tutti concordi nello stabilire quali rombi sono uguali e quali diversi.
Se due rombi (che non siano quadrati) hanno lo stesso lato ma l’angolo acuto di uno è diverso dall’angolo acuto dell’altro, possiamo essere certi che siano diversi?
Se due rombi (che non siano quadrati) hanno lo stesso lato e anche i due angoli acuti uguali, possiamo essere certi che siano uguali?
il teorema di pitagora e le terne pitagoriche
In una classe che abbia già studiato il teorema di Pitagora, “Rombi sul quaderno a quadretti” potrebbe aprirsi anche attraverso domande di questo tipo:
- La scelta della lunghezza del lato del rombo è stata casuale?
- Perché proprio 5 quadretti?
- Che cosa succede se invece di 5 quadretti scegliete un’altra lunghezza per i lati del rombo? Trovate più o meno di cinque rombi che si possono disegnare su carta a quadretti che abbiano il lato di quella lunghezza? Fate qualche esempio.
Un problema difficile
Disegnare un rombo con i lati che misurano esattamente cinque quadretti (e con i vertici negli incroci della quadrettatura) potrebbe essere considerato un esercizio persino abbastanza facile, visto il suggerimento contenuto nel testo.
Disegnare tutti i possibili rombi con queste caratteristiche è invece una richiesta degna di un problema significativo e “difficile”, ma alla portata dei ragazzi: i casi possibili sono forse più di quelli che ci si aspetta a prima vista, ma comunque non sono troppi!
I ragazzi potrebbero procedere per tentativi (e ben venga che lo facciano!), ma se ad un certo punto volessero essere certi di aver trovato tutti i possibili rombi con le caratteristiche richieste dovrebbero trovare un modo per rendere sistematica la loro ricerca, per essere cioè sicuri di non dimenticare alcun rombo.
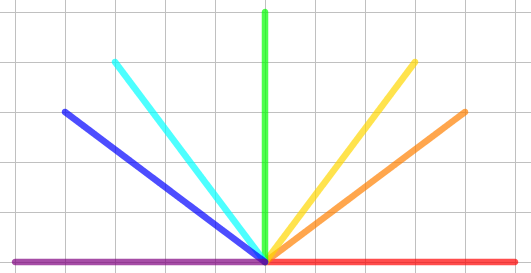
Una idea (non l’unica) che permette di sistematizzare la ricerca è quella di partire dai segmenti che su carta a quadretti possono essere disegnati, con inclinazioni diverse rispetto a una delle direzioni fissate dalle linee dei quadretti:
Poichè (fissata la lunghezza del lato), un rombo (che non sia un quadrato) è univocamente determinato dal suo angolo acuto, la ricerca di tutti i rombi possibili che soddisfano alle condizioni poste dal problema si riduce alla ricerca di tutti gli angoli acuti che si possono formare con due dei segmenti sopra disegnati.
Combinando questi segmenti in tutti i modi possibili ed eliminando i casi “doppi”, si ottengono cinque diversi angoli acuti e quindi cinque diversi rombi.
Scenari possibili
Con il suggerimento relativo alla lunghezza della diagonale di un rettangolo di lati 3 e 4 quadretti, questo problema può essere proposto in tutte le classi (comprese quelle che non abbiano ancora affrontato il teorema di Pitagora) in cui si voglia far emergere una discussione autentica a proposito di quando due poligoni (in particolare, due rombi) sono uguali e quando sono diversi.
“Rombi sul quaderno a quadretti” può essere un problema stimolante anche per ragazzi più grandi (ad esempio del primo biennio della scuola superiore), con l’aggiunta esplicita di argomentare le proprie risposte.
Materiale necessario
Sarà naturalmente indispensabile che i ragazzi abbiano a disposizione della carta a quadretti.
Uno strumento che (pur non essendo assolutamente “necessario”) potrebbe aiutare i ragazzi a porre attenzione al fatto che, in questo problema, si chiede che i triangoli abbiano i vertici negli incroci della quadrettatura è il geopiano.
Problema tratto da…
“Rombi sul quaderno a quadretti” riprende un problema proposto su Per non perdere la bussola di Marina Cazzola, pubblicato nel 2001 da Decibel editrice nella collana Quaderni a Quadretti.
Problemi collegati
Si tratta di un problema analogo a “Cosa si può fare con 5 quadretti“.