Biancaneve e i 77 funghi

Soluzione

Cucciolo ha ricevuto 8 funghi.

Commenti

Metacognizione

Biancaneve e i 77 funghi può essere una buona occasione per far riflettere gli alunni su alcuni atteggiamenti e accorgimenti che è utile assumere quando ci si trova di fronte ad un problema (di matematica).

Nella scuola primaria si cerca di abituare i bambini a scrivere i “dati” del problema, prima di iniziare a cercarne la soluzione. Questo problema può aiutare i ragazzini a capire che i “dati” non sono solo i “numeri scritti in cifre” presenti nel testo, bensì tutte le informazioni salienti in esso contenute, e che queste informazioni salienti possono essere registrate in tante maniere diverse: a volte è sufficiente trascriverle, ma altre volte può essere più utile evidenziarle nel testo, inserirle in una tabella, schematizzarle, riportarle in un grafico, tradurle in un disegno… Si tratterà, ogni volta, di trovare la maniera migliore possibile per rappresentare queste informazioni; ed è facile immaginare che ragazzi diversi, con esperienze diverse, in contesti diversi possano trovare più congeniali modi di rappresentazione diversi.

Questo problema può insegnare anche ad assumere un atteggiamento più aperto e creativo rispetto a quello di chi vorrebbe risolvere ogni cosa attraverso una serie di operazioni raggruppate in una espressione. Ben vengano le operazioni e ben vengano le espressioni, ma ben venga anche una sequenza di congetture e verifiche,  di tentativi e approssimazioni. E ben vengano strategie diverse, purché coerenti e motivate.

Strategie risolutive diverse

Una delle peculiarità di questo problema è l’abbondanza di strategie elementari attraverso le quali può essere risolto.

Tentativi nudi e crudi

Si può provare a vedere cosa succede assegnando a Cucciolo un numero di funghi “a caso” e, se il primo tentativo non va a buon fine, provare con un altro numero, finché non se ne trova uno che va bene. (Tra l’altro, come approfondiremo nel paragrafo seguente, difficilmente i ragazzini di scuola media scelgono altrettanto casualmente il secondo numero con cui provare: passano presto da un tentativo nudo e crudo a un tentativo ragionato).
Come insegnanti di matematica siamo forse portati a pensare che procedere per tentativi sia un modo troppo poco elegante di agire, forse anche troppo infantile, sicuramente poco efficiente in certe situazioni.  In realtà, piuttosto che gli alunni se ne stiano impauriti o addirittura paralizzati di fronte a un problema che non riescono ad incasellare in qualcosa che già sanno, ben venga che procedano a tentoni!
Nel procedere per tentativi, tra l’altro, è insita una questione che, quando si risolvono problemi, è di estrema importanza: quella della verifica, ossia di quella fase in cui, una volta trovata una soluzione, ci si riflette su, per decidere se è sensata oppure no, se rispetta i vincoli dati dal problema oppure no, se è realistica oppure no, e così via.
Si tratta di una fase tanto importante quanto trascurata, la cui necessità però spesso viene fatta emergere spontaneamente da quegli alunni che procedono per tentativi: provo ad assegnare 11 funghi a Cucciolo? Allora gli altri nani avranno 12, 13, 14, 15, 16 e 17 funghi. Si tratta di una soluzione? Non posso dirlo, se non prima di aver verificato che il totale dei funghi che ho così distribuito sia 77. Il fatto che 11+12+13+14+15+16+17 sia uguale a 98 mi dice che devo fare un altro tentativo.

tentativi “ragionati”

Procedere per tentativi, quindi, richiede innanzitutto di ragionare sulla coerenza della soluzione trovata rispetto alle condizioni date nel testo. Ma ci sono anche altri ragionamenti che devono o possono affiancare una strategia di questo tipo.
La più banale, che spesso i ragazzini mettono in atto, è questa: se al primo tentativo fatto il totale dei funghi che avrei distribuito supera 77, il mio secondo tentativo sarà con un numero più piccolo rispetto al primo, e viceversa. In questo modo posso avvicinarmi al risultato per approssimazioni successive.

Un altro ragionamento che abbiamo visto affiancare al procedere per tentativi è questo: una alunna ha provato a vedere che cosa sarebbe successo assegnando 7 funghi a Cucciolo e, di conseguenza, 8, 9, 10, 11, 12 e 13 funghi agli altri nani. Si è accorta che in questo modo il totale dei funghi distribuiti sarebbe stato 7+8+9+10+11+12+13=70, ma non si è limitata ad accorgersi che (essendo 70<77) avrebbe dovuto provare con un numero maggiore di funghi. Ha calcolato la differenza tra il numero di funghi da distribuire e quelli effettivamente distribuiti con questo tentativo: poiché 77-70=7 ci sono ancora 7 funghi da distribuire. Affinché la differenza di funghi assegnati tra i nani rimanga la stessa, questi 7 funghi vanno distribuiti in parti uguali, quindi uno a testa. Quindi i funghi da dare a Cucciolo saranno 8.
Un ragionamento analogo si può fare qualunque sia il numero scelto inizialmente “a caso”.
Questo esempio ci sembra dimostri che valga la pena incentivare i ragazzi a procedere per tentativi, quanto meno quando non hanno altre idee, perché questo può permettere loro di entrare dentro il problema, di comprenderlo meglio ed, eventualmente, di trovare una strategia che non necessiti troppe altre prove. Tutto questo è possibile se si affronta il problema con sufficiente tenacia e determinazione (abituandosi al fatto che non sempre si trova la soluzione al primo tentativo e che questo non ci deve scoraggiare) e se non si rinuncia a tenere gli occhi ben aperti e a usare la testa (per guardare dove ci portano i diversi tentativi messi in atto e muoverci di conseguenza).

disegni, espressioni, equazioni

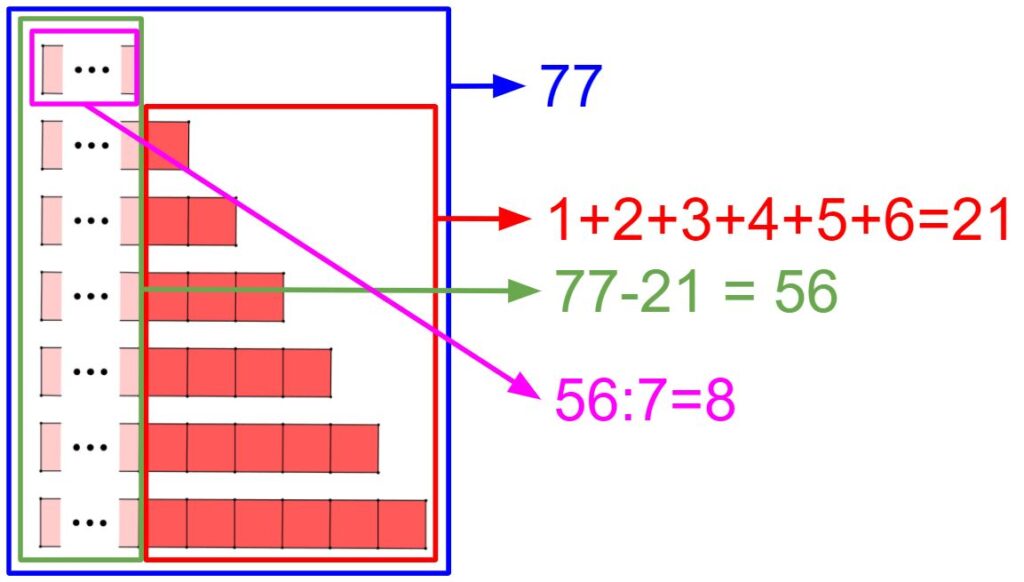
Se la maggior parte degli alunni inizia con l’assegnare un ipotetico numero di funghi a Cucciolo e ragiona sul che cosa succede di conseguenza, ci sono anche alunni che prendono in considerazione come prima cosa i funghi che gli altri nani ricevono in più rispetto a Cucciolo. Un nano riceve 1 fungo in più di Cucciolo, un secondo nano ne riceve 2 in più di Cucciolo, un terzo nano ne riceve 3 in più di Cucciolo e così via fino al sesto nano che ne riceve 6 in più di Cucciolo: il totale dei funghi distribuiti tra questi sei nani “in più” oltre a quelli che ha ricevuto anche Cucciolo è allora uguale a 1+2+3+4+5+6 cioè uguale a 21. I rimanenti funghi, che sono 77-21=56, vengono distribuiti in parti uguali. I funghi assegnati a Cucciolo sono quindi 56:7=8.

Altri alunni hanno usato la stessa strategia e l’hanno scritta attraverso una unica espressione: [77-(1+2+3+4+5+6)]:7.

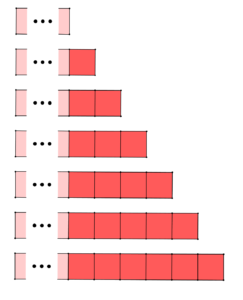
Alcuni alunni, prima di scrivere questi calcoli, hanno fatto un disegno in cui hanno rappresentato su ciascuna riga la quantità di funghi assegnata ad un nano: accanto a una certa quantità di funghi ignota (rappresentata in rosa), ci sono quelli ricevuti in aggiunta rispetto a Cucciolo (ogni quadratino rosso rappresenta un fungo).

A partire dal disegno hanno poi svolto gli stessi calcoli descritti in precedenza:

Di fatto, questo disegno è un modo come un altro per rappresentare l’equazione
c+(c+1)+(c+2)+(c+3)+(c+4)+(c+5)+(c+6)=77
in cui c rappresenta il numero di funghi assegnati a Cucciolo. Sul disegno, di fatto, si possono anche leggere tutti i passaggi con cui questa equazione può essere risolta:
7c+21=77
7c=77-21
7c=56
c=56:7
c=8.

un altro disegno, un’altra espressione

Analoga ma non completamente uguale alla precedente è la strategia di chi ha considerato che Cucciolo dovesse ricevere almeno 1 fungo e quindi gli altri nani rispettivamente almeno 2, 3, 4, 5, 6 e 7. E che poi gli altri funghi andassero equamente distribuiti tra i nani.

Qualcuno è partito facendo un disegno:

In rosa, sono rappresentati i funghi inizialmente distribuiti ai nani, in tutto 1+2+3+4+5+6+7=28.
Poiché 77-28=49, si possono distribuire altri 49:7=7 funghi a testa.
A Cucciolo vanno allora 1+7=8 funghi.

Anche le operazioni qui descritte possono essere inserite in un’unica espressione:
1+[77-(1+2+3+4+5+6+7)]:7

l’errore e la media

Non di rado qualche ragazzino crede di risolvere questo problema attraverso una divisione e risponde che Cucciolo riceve 11 funghi perché 77:7=11.

Dietro un errore di questo tipo può esserci una lettura affrettata o la mancata comprensione di come effettivamente vengano suddivisi i funghi tra i vari nani. Ma può esserci anche la convinzione che ogni problema assegnato dall’insegnante di matematica debba potersi risolvere facendo una operazione (a scelta tra addizione, sottrazione, moltiplicazione e divisione) tra i dati numerici presenti nel problema; e poiché il testo dice che Biancaneve divide i funghi tra i nani, la scelta degli alunni ricade sulla divisione.

Per persuadere gli alunni del fatto che questa soluzione non è corretta, basta verificare quanti funghi riceverebbe ciascun nano e mostrare che, in questo modo, i funghi distribuiti sarebbero ben più di 77.

In alcune delle classi in cui è stato proposto questo problema, però, alcuni alunni hanno giustamente interpretato il risultato della divisione 77:7 non come il numero dei funghi ricevuti da Cucciolo, quanto come la media dei funghi ricevuti da ciascun nano. Se avessero ricevuto tutti lo stesso numero di funghi, i nani avrebbero ricevuto 11 funghi a testa. In realtà, però, un solo nano ha ricevuto 11 funghi: il nano che si pone esattamente a metà dell’ipotetica fila nella quale ognuno riceve un fungo in più di quello precedente. I nani dopo di lui riceveranno rispettivamente 1, 2 e 3 funghi in più, mentre quelli prima di lui riceveranno 1, 2 e 3 funghi in meno. Cucciolo, quindi, che è il nano che ha ricevuto meno funghi, avrà ricevuto 11-3=8 funghi.
Questa è una strategia risolutiva che, se emerge dagli alunni, andrebbe valorizzata per almeno due motivi:

• mette in luce quanto di buono, sensato e significativo è presente nell’errore che può aver commesso qualche compagno nel dire che Cucciolo ha avuto 77:7=11 funghi;
• mette in risalto la simmetria del problema (non certo rispetto a Cucciolo, ma rispetto al nano “di mezzo”) e il fatto che, riflettendo su questa simmetria e indicando con x il numero dei funghi ricevuti dal nano “di mezzo”, si può rappresentare il problema attravero l’equazione 7x=77, un po’ più semplice di quella vista prima.

Un problema aperto

Dopo aver condiviso le diverse strategie utilizzate dagli alunni per risolvere questo problema, può essere utile porsi con i ragazzi alcune ulteriori domande, per capire quanto le diverse strategie sono “generalizzabili” e quanto gli alunni le abbiano davvero comprese. Alcune domande utili a questo scopo potrebbero essere:

• Se avesse avuto 87 funghi, Biancaneve avrebbe potuto distribuire tutti i funghi dandone un certo numero a Cucciolo, uno in più a Mammolo, ancora uno in più a Brontolo e così via?
• Quanti devono essere in totale i funghi affinché Biancaneve possa procedere nel modo descritto dal problema?
• Se Biancaneve avesse voluto tenere dei funghi anche per sè, mettendosi come ottava della fila, quanti avrebbero dovuto essere i funghi per permetterle di procedere nello stesso modo?

Sperimentazione e possibili scenari

Questo problema è stato sperimentato per diversi anni nelle classi prime degli iscritti ai corsi MathUp per insegnanti della scuola secondaria di primo grado.  Si è rivelato utile anche nelle classi terze dello stesso segmento scolastico, classi in cui tipicamente si introducono le equazioni di primo grado e si introducono problemi con esse risolubili.

Problema tratto da…

Biancaneve e i 77 funghi è nato come “gioco matematico” da proporre ai bambini della scuola primaria: si trova come gioco n. 2 a pagina 6 del volume La formica e il miele di Isabella Bonaiti, Lidia Chiesa e Simona Lanfranchi (Mimesis, 2005).