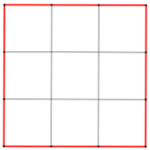
Partiamo da un quadrato, mettendone in evidenza i lati (in figura colorati in rosso); tagliamolo in quadratini, dividendo ogni lato in tre parti uguali; come vediamo dalla figura, dei 9 quadratini ottenuti, uno non ha lati rossi, 4 hanno un solo lato rosso, 4 ne hanno due e nessuno ne ha più di due.
Andiamo avanti e tagliamo il quadrato in quadratini dividendo ogni lato in 4 parti uguali: quanti quadratini si ottengono? quanti senza lati rossi? quanti con un solo lato rosso? quanti con due lati rossi? quanti con più di due? E se si parte dalla divisione di ogni lato in 5 parti uguali? E in 10? e in 57? In quest’ultimo caso non ci interessa che calcoliate il numero esatto; vorremmo però che indicaste quali operazioni occorre fare per calcolarlo.
Se avete risposto in modo convincente alle ultime domande, non avrete difficoltà a dire che cosa succede tagliando un quadrato in quadratini a partire da una divisione del lato in n parti uguali: n è un numero, intero, positivo, solo che… non sappiamo di che numero si tratta; quindi le operazioni che indicate sul numero n (per ottenere il numero totale di quadratini e il numero di quelli con nessuno, o 1, o 2 lati rossi) devono “funzionare” per qualunque numero. Avete finito? E ora come potreste controllare l’esattezza della vostra risposta?
Soluzione
Nella prima colonna della tabella sottostante, riportiamo in verde i valori che nel testo sono già dati; nelle altre colonne quelli che gli alunni dovranno determinare.
| numero di parti in cui è diviso ogni lato | 3 | 4 | 5 | 10 | 57 | n |
| numero di quadratini | 9 | 16 | 25 | 100 | 572 | n2 |
| numero di quadratini senza lati rossi | 1 | 4 | 9 | 64 | 552 | (n-2)2 |
| numero di quadratini con 1 lato rosso | 4 | 8 | 12 | 32 | 55×4 | (n-2)x4 |
| numero di quadratini con 2 lati rossi | 4 | 4 | 4 | 4 | 4 | 4 |
| numero di quadratini con più di 2 lati rossi | 0 | 0 | 0 | 0 | 0 | 0 |
Commenti
Al primo livello diamo noi il risultato e invitiamo i ragazzi a “leggerlo” nella figura. Poi dovranno essere loro a esplorare gli stadi successivi. Nei primi stadi (3,4,5) ci aspettiamo che i ragazzi facciano una figura e contino direttamente sulla figura i quadratini dei diversi tipi.
Quando i numeri diventano più grandi comincia a essere noioso contare e prevediamo che qualche ragazzo si accorga, già col quadrato il cui lato viene diviso in 10 parti uguali (o magari anche prima), dei seguenti fatti:
- i quadratini con due lati rossi sono (sempre!) 4 perché sono in corrispondenza dei vertici del quadrato;
- non ci sono mai quadratini con più di due lati rossi;
- i quadratini con un solo lato rosso sono sul bordo esterno del quadrato (escludendo i vertici), quindi per ogni lato ce ne sono 8 (=10-2) e in totale saranno 32 (=4×8);
- i quadratini senza lati rossi sono quelli centrali, che formano un quadrato il cui lato ha due caselle in meno del quadrato originale, e quindi sono 64 (=82).
E possono avere conferma di aver proceduto correttamente dal fatto che 64+32+0+4=100.
Un conto fatto in questo modo apre la strada senza difficoltà a dire che, quando il lato viene diviso in 57 (rispettivamente, n) parti uguali, i quadratini in totale sono 572 (rispettivamente, n2 ), i quadratini senza lati rossi sono (57-2)2 (rispettivamente, (n-2)2 ), i quadratini con un solo lato rosso sono 4x(57-2) (rispettivamente, 4x(n-2)) e quelli con due lati rossi sono 4.
Certo non è questa l’unica via che i ragazzi possono utilizzare; alcuni potranno anche, magari a partire da una tabella come una di quelle rappresentate qui sopra (fornita dall’insegnante con i soli contenuti della prima colonna o predisposta dagli stessi alunni), cominciare a completare le prime colonne, in corrispondenza della divisione del lato in 4 o 5 parti uguali e poi osservare le righe:
- 9, 16, 25, … “viene voglia di” continuare con 36, 49 ecc., cioè il quadrato del numero nella prima riga;
- 1, 4, 9, … “viene voglia di” continuare con 16, 25 eccetera, cioè di nuovo un quadrato, ma non proprio del numero corrispondente nella prima riga, bensì…;
- 4, 8, 12, … “viene voglia di” continuare con la tabellina del 4, quindi 4x…;
- 4, 4, 4, … qui è fin troppo facile l’idea di continuare sempre con 4, così come di continuare sempre con 0 nella riga successiva.
Naturalmente il fatto che “venga voglia di” continuare in un certo modo non garantisce certo che quella sia l’unica possibilità, né che, fra le tante, sia quella che si attaglia al problema. Ma, se qui abbiamo un po’ di fortuna, proprio la discussione fra i ragazzi, magari fra chi ha visto le cose in un modo e chi le ha viste in un altro, potrebbe far scattare una consapevolezza diversa: ci accorgiamo così che non è solo che “ci viene voglia di” continuare in un certo modo, ma è proprio la costruzione che viene “tradotta” algebricamente in queste operazioni.
L’ultima domanda è importante e sarebbe utile che i ragazzi acquisissero sistematicamente l’abitudine di verificare l’esattezza delle loro risposte. Qui (riferendosi all’ultima domanda con la lettera n variabile), potrebbero intanto controllare quali numeri risultino nel caso n=3, o n=4 (o anche n=2, quando il quadrato è diviso in 4 quadratini, tutti con due lati rossi) e verificare che riottengono i valori che già hanno trovato in quei casi.
Un altro controllo che potrebbero fare consiste nel sommare i tre termini ottenuti (per i casi di nessun lato rosso, un lato rosso, due lati rossi) per verificare che la loro somma sia proprio n2 . E non c’è bisogno di “calcolo letterale con monomi e polinomi” o di “prodotti notevoli”! Basta usare le proprietà delle operazioni (in particolare la proprietà distributiva) per accorgersi che:
4 + 4(n– 2) + (n– 2) (n– 2) = 4 + 4n – 8 + n2 -2n -2n +4 = n2 .
Poi, più avanti, quando si impadroniranno del calcolo letterale, potranno riconoscere nella somma dei tre addendi sulla sinistra il “prodotto notevole” (2+(n-2))2.
Una delle possibilità per utilizzare questo problema è (nella direzione di un avvio all’algebra) quella di testare le potenzialità dei ragazzi nel riconoscimento di una costruzione che continua sempre uguale; e di come l’utilizzo di una lettera al posto dei numeri possa essere prezioso per descrivere una situazione di questo tipo.
Sperimentazione e possibili scenari
Nell’anno scolastico 2017 / 2018 abbiamo potuto osservare le soluzioni di questo problema proposte dagli alunni di sessanta classi terze della scuola secondaria di primo grado.
Oltre a molte delle cose già dette, è stato interessante notare come pochissimi gruppi di alunni abbiano raccolto il suggerimento relativo alla suddivisione del lato in 57 parti uguali: “non ci interessa che calcoliate il numero esatto; vorremmo però che indicaste quali operazioni occorre fare per calcolarlo”. Quasi tutti i gruppi hanno preferito svolgere il calcolo, piuttosto che lasciare indicato 552, 572, 55×4, quasi a indicare la convinzione che la risposta alla domanda di un problema debba sempre per forza essere un numero.
Il problema è stato proposto anche in alcune classi prime della scuola secondaria di secondo grado; in queste classi “Affettare un quadrato” è stato prezioso innanzitutto per far toccare con mano ai ragazzi come l’utilizzo delle lettere ci venga in aiuto per descrivere situazioni come questa, in cui c’è una struttra che si ripete con regolarità ma anche in funzione di qualcosa che varia: un avvio, dunque, al concetto di funzione. Gli alunni di queste classi hanno potuto, con maggior facilità di quelli della scuola secondaria di primo grado, lavorare sulle espressioni letterali ottenute al fine di verificare l’esattezza delle loro risposte.
Ci immaginiamo che “Affettare un quadrato” possa essere proposto con successo anche in classi quinte della scuola primaria o in classi prime e seconde della scuola secondaria di primo grado nell’ottica di un graduale avvio all’algebra, eventualmente sostituendo la domanda finale (il caso generale in cui il lato del quadrato è diviso in n parti uguali) con un’altra, in cui i il lato del quadrato sia diviso in un numero di parti uguali così grande da incoraggiare i ragazzini a lasciare indicate le operazioni invece di effettuare il calcolo: inserire in un problema una domanda finale con numeri grandi, ma con la possibilità di lasciare indicate le operazioni, costituisce già di per sè un avvio all’uso delle lettere.
Problema tratto da…
Questo problema è stato proposto tra i “problemi iniziali” della sperimentazione legata al corso MathUp per la classe terza della Scuola secondaria di primo grado nell’anno scolastico 2017 / 2018.
Problemi collegati
Possibili varianti possono essere considerati i problemi Affettare un cubo e Affettare un triangolo, di prossima pubblicazione.