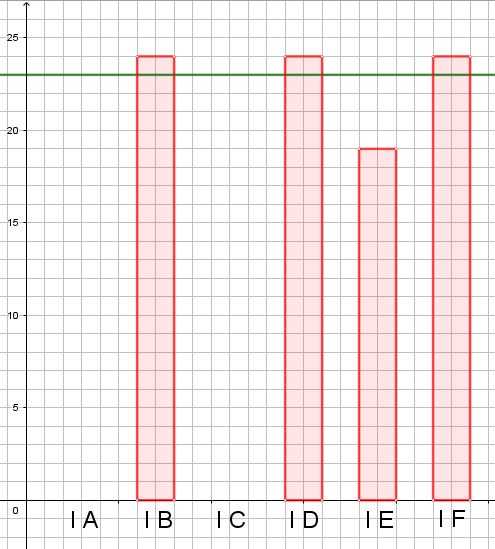
Navigando nel sito della scuola, Karim legge che la media di alunni per classe nelle 6 classi prime è di 23. Karim sa che in ciascuna delle classi 1a B, 1a D e 1a F ci sono 24 alunni e che nella classe 1a E ci sono 19 alunni.
Secondo voi è possibile sapere con certezza quanti alunni ci sono in 1a A e quanti alunni ci sono in 1a C? Motivate la vostra risposta.
Alla sua amica Giovanna sembra di ricordare che sono 21 in 1a A e 22 in 1a C.
Secondo voi è possibile? Perché?
In effetti Giovanna ricorda bene a metà!
Se ha ricordato bene che ci sono 21 alunni in 1a A, tenendo conto che la media degli alunni delle classi prime è 23, quanti alunni ci dovrebbero essere in 1a C?
Se invece ha ricordato bene che ci sono 22 alunni in 1a C, tenendo sempre conto che la media degli alunni delle classi prime è 23, quanti alunni ci dovrebbero essere in 1a A?
Soluzione
Non è possibile sapere con certezza quanti alunni ci sono in 1a A e quanti ce ne sono in 1a C: possiamo solo sapere che la somma dei numeri degli alunni delle due classi è 47, ma esistono diverse coppie di numeri naturali che hanno somma 47 e che possono ragionevolmente rappresentare il numero degli alunni della 1a A e della 1a C.
Non è possibile che ci siano 21 alunni in 1a A e 22 alunni in 1a C; se così fosse, la media degli alunni per classe sarebbe uguale a (21+24+22+24+19+24):6 e quindi inferiore a quella riportata sul sito della scuola.
Se Giovanna ha ricordato bene che ci sono 21 alunni in 1a A, tenendo conto che la media degli alunni delle classi prime è 23, in 1a C ci dovrebbero essere 26 alunni.
Se Giovanna invece ha ricordato bene che ci sono 22 alunni in 1a C, tenendo sempre conto che la media degli alunni delle classi prime è 23, in 1a A ci dovrebbero essere 25 alunni.
Commenti
Un problema significativo
È facile che i bambini abbiano già incontrato il concetto di media nella vita quotidiana, ancor prima che a scuola.
Questo fatto può costituire una ricchezza, perché può far sì che l’idea di media, formatasi a seguito di esperienze concrete, trovi in esse senso e significato, e si sviluppi fino a diventare un concetto sì astratto, ma ricco di sostanza.
In alcuni casi, però, la scarsa numerosità (e ancor più la scarsa varietà) di queste esperienze concrete e soprattutto di opportune riflessioni su di esse, fanno sì che nei bambini si formi un’idea un po’ distorta (o quantomeno incompleta) di che cosa la media sia e di quali informazioni porti con sé. Per esempio: alcuni bambini, abituati a calcolare la media esclusivamente di due valori, sono convinti che la media di un certo numero di dati si ottenga sempre dividendo a metà la somma di quei dati, indipendentemente da quanti essi siano; altri bambini (forse per lo stesso motivo), sono convinti che la media sia sempre equidistante dal più grande e dal più piccolo dei dati considerati; altri ancora (probabilmente perché hanno visto questa cosa accadere in tutti i pochi esempi concreti con cui hanno avuto a che fare) sono convinti che sia possibile calcolare la media solo di valori molto vicini tra loro.
Ecco allora che un problema come Quanti alunni per classe? può venire in aiuto all’insegnante per fare in modo che bambini e ragazzi diventino sempre più consapevoli del significato della media e non solo di come fare a calcolarla a partire da certi dati.
Un percorso a ritroso
Una delle caratteristiche che rendono questo problema adatto a far riflettere alunni e alunne sul significato della media è il fatto che si tratta di un “problema inverso” rispetto a quelli che più frequentemente si trovano sui libri di testo: la media degli alunni per classe è nota, mentre non si sa quanti alunni ci siano esattamente in ciascuna classe.
Non pochi degli alunni cui è stato proposto questo problema, anche se sapevano bene come si calcola la media aritmetica, si sono trovati spiazzati di fronte alla prima domanda perché pensavano che (come hanno scritto gli alunni di un gruppo che ha sperimentato il problema nel 2021) “se Karim ha calcolato la media delle classi, sa anche il numero degli alunni della 1a A e della 1a C“. Questo immaginarsi che, per sapere la media di certi valori, sia indispensabile conoscerli uno a uno, dimostra che non si ha piena consapevolezza di che cosa sia la media (nemmeno a livello intuitivo) e che la si identifica con la formula imparata per calcolarla.
Il problema Quanti alunni per classe? aiuta gli alunni a far luce sul concetto di media, proprio perché per risolverlo non basta sapere a memoria che “la media aritmetica degli alunni delle classi si calcola dividendo la somma dei numeri degli alunni di ciascuna classe per il numero delle classi”. Bisogna guardare oltre la formula, per accorgersi di uno dei seguenti fatti, o di altri equivalenti:
- la media degli alunni per classe è un rapporto in cui il numeratore (la somma dei numeri degli alunni di ciascuna classe prima) è semplicemente il totale degli alunni di tutte le classi prime della scuola;
- la media degli alunni per classe è il numero di alunni che avrebbe ciascuna classe se le classi fossero equi-numerose.
(Per inciso: con alcuni alunni che più di altri faticavano a immaginare che si potesse conoscere la media senza conoscere i singoli valori è stato efficace sospendere la riflessione su questo problema per introdurne a bruciapelo un altro. “Enrico cucina per sé e i suoi due figli Filippo e Alvise 400 g di spaghetti. Non rimangono avanzi. Quanta pasta hanno mangiato in media Enrico, Filippo e Alvise?”)
Strategie risolutive diverse
Nessuna certezza
I gruppi di alunni che hanno risposto correttamente alle prime richieste del problema hanno usato strategie diverse, per arrivare alla soluzione.
In alcuni gruppi è parso chiaro fin dall’inizio che dire “in media ci sono 23 alunni per classe” è come dire che – se le 6 classi avessero tutte lo stesso numero di alunni – avrebbero 23 alunni ciascuna; da qui a calcolare il totale degli alunni delle classi prime il passo è stato breve: 23×6 = 138.
Per sottrazione, sono arrivati alla somma degli alunni delle classi 1a A e 1a C:
138-(24+24+24+19) = 138-91 = 47.
A questo punto vari gruppi hanno notato che il totale di 47 alunni nelle due classi può essere raggiunto in modi diversi; è interessante notare che tutti si sono mantenuti su numeri “plausibili”, alcuni esplicitando il fatto che le classi non possono – per legge – avere più di 30 alunni, altri semplicemente proponendo soluzioni che mantenessero i numeri degli alunni della 1a A e della 1a C prossimi a quelli delle altre sezioni. Forse perché la contestualizzazione di questo problema è molto vicina all’esperienza dei ragazzi, è venuto loro spontaneo fornire soluzioni che non fossero solo corrette dal punto di vista della matematica, ma che fossero anche coerenti con la realtà in cui il problema è ambientato.
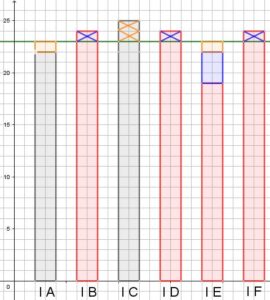
Altri gruppi hanno cercato di “parificare” i numeri delle varie classi. Alcuni ragazzi sono partiti da un grafico simile a quello ricostruito qui sotto
e hanno cercato di avvicinare il più possibile i numeri degli alunni, rappresentati dalle altezze delle colonne del grafico, alla media, rappresentata dalla linea verde.
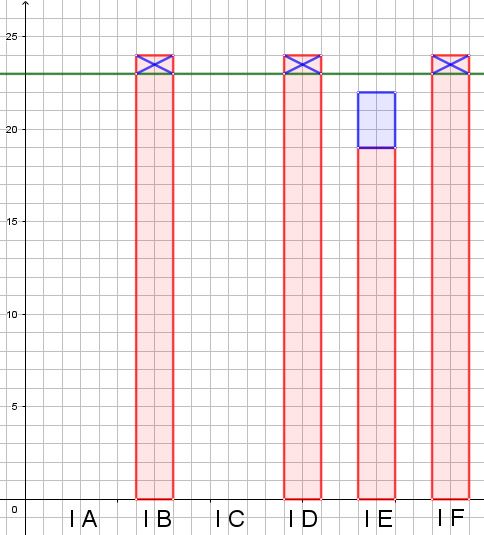
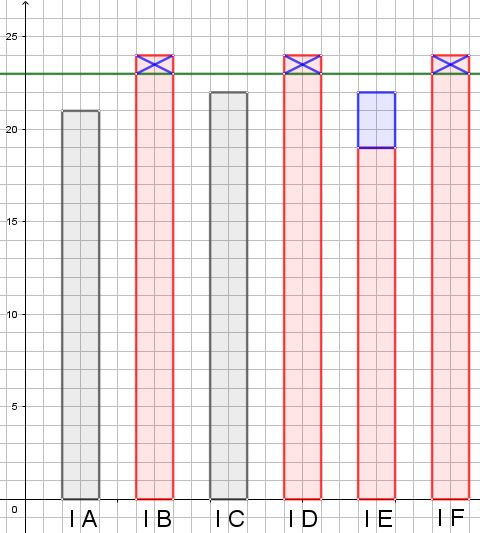
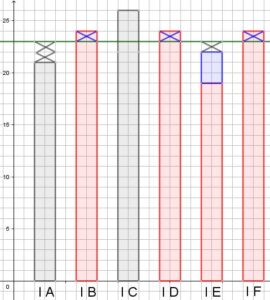
Hanno dunque immaginato di togliere 1 alunno da ciascuna classe con 24 alunni (perché ciascuna di esse ha 1 alunno in più della media) e di dare questi alunni alla classe con 19 alunni trasformandola così in una classe da 22 alunni. Osservando solo le classi 1a B, 1a D, 1a E e 1a F si è quindi in difetto di 1 alunno rispetto alla media e questo significa che le altre due classi dovranno avere, nel complesso, 1 alunno in eccesso rispetto alla media (e quindi potranno essere una di 23 e l’altra di 24 alunni, oppure una di 22 e l’altra di 25 alunni, e così via).
i falsi ricordi di Giovanna
Per valutare la plausibilità del ricordo di Giovanna (ossia che ci siano 21 alunni in 1a A e 22 alunni in 1a C) alcuni alunni hanno semplicemente calcolato il totale degli alunni delle classi prime
21+24+22+24+19+24 = 134
e si sono accorti che esso non è compatibile con il totale che avevano calcolato in precedenza a partire dalla media
23×6 = 138.
Altri alunni si sono spinti fino a calcolare la media complessiva
(21+24+22+24+19+24):6 = 134:6 = 22+⅓
e si sono accorti (quando non hanno distrattamente approssimato alle unità o sbagliato il calcolo) di non ottenere la media fornita dal problema.
Altri ancora hanno continuato a lavorare sui numeri degli alunni delle classi, mostrando che, anche ridistribuendo gli alunni delle classi più numerose, se entrambe le classi in questione hanno un numero di alunni inferiori alla media, non è possibile che la media complessiva risulti 23.
i ricordi buoni a metà
Anche per rispondere alle ultime domande del problema, gruppi diversi hanno usato strategie diverse.
C’è chi ha impostato delle espressioni:
- se ci sono 21 alunni in 1a A, allora in 1a C gli alunni dovranno essere 23×6-(21+24+24+19+24) = 138-112 = 26
- se ci sono 22 alunni in 1a C, allora in 1a A gli alunni dovranno essere 23×6-(24+22+24+19+24) = 138-113 = 25
C’è chi ha di nuovo lavorato (direttamente sui numeri o passando per un grafico) al fine di pareggiare i conti tra le classi, ottenendo che
- se in 1a A gli alunni sono 21, cioè 2 meno della media, essendoci nel complesso delle classi 1a B, 1a D, 1a E e 1a F già un difetto di 1 rispetto alla media, gli alunni della 1a C dovranno essere 2+1=3 in più della media, ossia 23+3=26;
- se in 1a C gli alunni sono 25, cioè 2 più della media, essendoci nel complesso delle classi 1a B, 1a D, 1a E e 1a F già un difetto di 1 rispetto alla media, gli alunni della 1a C dovranno essere 2-1=1 in meno della media, ossia 23-1=22.
Altri gruppi infine hanno proceduto per tentativi, provando ad aggiungere numeri diversi ai cinque noti, fino a che ne trovavano uno per il quale, dividendo il totale per 6, ottenevano proprio 23.
Procedere per tentativi va benissimo, soprattutto se non si ha (o non si ha
ancora) a disposizione un metodo più efficace: questo dobbiamo sottolinearlo ai nostri alunni, che troppo spesso si bloccano di fronte a problemi per risolvere i quali non sanno esplicitare a priori un procedimento diretto.
Procedere per tentativi va benissimo, ancor più quando si tratta di tentativi ragionati (e non buttati là a casaccio), che vengono sostituiti da altri tentativi man mano che si riflette sugli errori. E, se si è andati per tentativi ed errori, ragionandoci sopra, diventa poi naturale alla fine ripensare alla soluzione e cercare di capire se, a posteriori, si riesce magari a trovare una maniera più “economica” per raggiungerla. Questa maniera più “economica” (cioè che richiede meno tempo, o meno calcoli, o semplicemente ci espone meno al rischio di errori) potrebbe tornare utile in un’occasione successiva e, a volte, può anche farci scoprire uno strumento matematico nuovo.
Un problema difficile
difficoltà linguistiche o matematiche?
L’impressione che abbiamo avuto nelle classi che hanno sperimentato questo problema è che le difficoltà maggiori si siano riscontrate nel momento in cui i ragazzi dovevano giustificare le proprie risposte, descrivere i propri ragionamenti e spiegare che cosa avevano fatto.
Parte di questa difficoltà degli alunni dipende probabilmente dalla poca consapevolezza degli strumenti che stanno usando e dalla difficoltà di capire quando un calcolo è già esplicativo di un ragionamento e quando invece vada accompagnato da una ulteriore spiegazione.
A volte però si ha la netta impressione che la difficoltà stia più nell’uso della lingua italiana che in quello degli strumenti della matematica: i ragazzi lasciano molti sottintesi, non rileggono quanto scrivono, o quantomeno non sembrano chiedersi se ciò che hanno scritto può essere comprensibile per chi non era presente nel momento in cui loro discutevano, facevano calcoli, si interrogavano e si rispondevano a vicenda.
Non è insolito, e non c’è da scoraggiarsi: imparare ad esprimersi e a curare il processo di scrittura del proprio pensiero necessita di un percorso lungo e complicato, che richiede tempo e lentezza. L’insegnante deve accompagnare gli alunni in questo percorso, cercando sempre di capire cosa vogliono dire, ma anche rifiutandosi di trasformarsi in un indovino per poterlo fare!
Una strategia utile è quella di fare in modo che i ragazzi debbano spiegare i propri ragionamenti non tanto all’insegnante che li conosce bene o a un compagno che ha seguito tutta la lezione, quanto a un insegnante esterno alla classe, o a un compagno assente. Che si tratti di realtà o finzione, questo dà una motivazione in più agli alunni per mettersi alla ricerca di un modo efficace di esprimersi.
errori illuminanti
Come spesso accade quando si propone un bel problema, anche in questo caso il lavoro di alcuni gruppi di alunni ha fatto emergere alcuni errori preziosi, perché hanno posto l’accento su alcuni fraintendimenti che è stato bene non siano rimasti sotto traccia.
- Nel rispondere alla domanda relativa alla plausibilità dei ricordi di Giovanna, un gruppo di alunni ha scritto: “Sì, è possibile che in 1a A ci siano 21 alunni e in1a C ce ne siano 22, perché i numeri 21 e 22 sono vicini al 23″. Questa risposta ha fatto emergere il convincimento (errato) che la media sia un valore vicino a tutti i dati raccolti, cosa che invece non è scontata.
- Nel rispondere alle ultime domande, un gruppo di alunni ha scritto: “Se in 1a A gli alunni sono 21, allora in 1a C gli alunni devono essere 25, perché così la media è (21+25):2 = 46:2 = 23 come dovrebbe essere. Questa risposta ha fatto emergere il convincimento (errato) che le medie parziali debbano coincidere con la media complessiva, cosa che non è affatto vera.
Sperimentazione e possibili scenari
Il problema Quanti alunni per classe? è stato proposto ai corsisti e alle corsiste che hanno seguito il corso MathUp “Problemi di matematica: un gioco da ragazzi” sia nell’anno scolastico 2021 / 2022 (nella tappa dedicata al processo del Contare) che (in una forma lievemente diversa) nell’anno scolastico 2024 / 2025 (nella tappa dedicata al tema della Media), in entrambi i casi perché lo sperimentassero nella classe prima della scuola secondaria di primo grado.
Proprio per quanto si diceva nei commenti a proposito del fatto che i bambini vengono in contatto con l’idea di media molto presto, crediamo che possa essere proposto anche alle classi quinte della scuola primaria.
Problema tratto da…
Il problema è ispirato a uno dei quesiti della Prova Nazionale somministrata dall’INVALSI nel 2014 agli studenti della classe terza della scuola secondaria di primo grado:
Il quesito sopra riportato, come il problema Quanti alunni per classe?, presenta la difficoltà di fornire la media di alcuni dati e di chiedere informazioni su questi dati (invece di fare il viceversa, come capita più spesso). Il fatto di essere un quesito chiuso, con quattro risposte possibili tra le quali sceglierne una sola corretta, lo rende però nettamente più semplice del problema aperto.
Nel caso della Prova Nazionale del 2014, infatti, gli alunni potevano semplicemente usare per quattro volte la formula per il calcolo della media, senza fare ulteriori riflessioni, usando ciascuna volta uno diverso dei numeri dati tra le possibili risposte, per vedere con quale valore si ottenesse la media fornita dal testo. E infatti, nel 2014, i risultati nazionali hanno presentato il 61,2% di risposte esatte (la risposta B), il 37,2 % di risposte errate (e precisamente il 10,5% di risposte A, il 19% di risposte C e i 7,7% di risposte D) e l’1,6% di risposte non date o non valide.