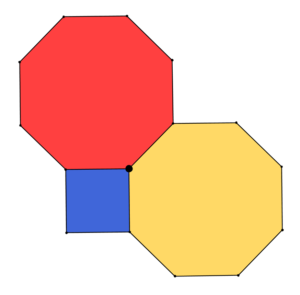
Nella figura qui sotto vedete tre poligoni regolari, due ottagoni e un quadrato, che hanno in comune un vertice e che riempiono perfettamente, senza sovrapposizioni e senza buchi, l’angolo giro intorno a quel vertice.
Riccardo, che in questo periodo sta studiando le frazioni, vedendo la figura su un libro, esclama “To’! Nella figura riesco a vedere che 3/8 + 3/8 + 1/4 = 1”.
Riccardo ha ragione! Nella figura si può “leggere” che l’intero angolo giro è la somma di tre angoli: un angolo retto (l’angolo del quadrato) e due angoli uguali all’angolo interno di un ottagono regolare. L’angolo del quadrato è 1/4 dell’angolo giro, mentre quello dell’ottagono regolare è 135°, cioè i 3/8 dell’angolo giro, quindi è proprio vero che 3/8 + 3/8 + 1/4 = 1.
Sapreste trovare almeno altre tre diverse maniere di accostare dei poligoni regolari (non tutti uguali fra loro!) in modo che riempiano l’angolo giro intorno a un punto?
E sapreste “leggere” nelle vostre figure delle somme di frazioni che danno come risultato 1?
Un suggerimento: vi può aiutare sapere che l’angolo interno di un poligono regolare di n lati, espresso come frazione dell’angolo giro, è (n-2)/2n.
Soluzione
Si tratta di scrivere 1 come somma di frazioni del tipo:
1/6, 2/8, 3/10, 4/12, 5/14, 6/16, …. , (n-2)/2n.
Ai ragazzi chiediamo solo di dare qualche esempio (almeno tre). Tutte le soluzioni possibili sono elencate più sotto, nel paragrafo Una pluralità di soluzioni.
Commenti
Il suggerimento che viene dato alla fine del testo del problema (e cioè il fatto che l’angolo di un poligono regolare di n lati, espresso come frazione dell’angolo giro, è proprio (n-2)/2n) è un po’ il cuore del problema e rappresenta il ponte tra aritmetica e geometria. Non è nemmeno difficile da giustificare, se magari qualche ragazzo si incuriosisce e si domanda da dove spunta questa frazione. Si può partire da un triangolo (qualsiasi, non necessariamente regolare), in cui sappiamo che la somma degli angoli è un angolo piatto, ovvero 1/2 dell’angolo giro. Un qualsiasi poligono di n lati si può scomporre in n-2 triangoli (per esempio usando le n-3 diagonali uscenti da un vertice).
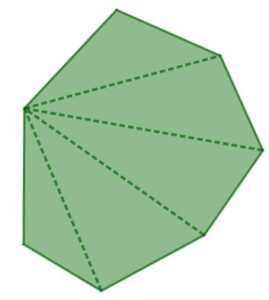
Osservando questa scomposizione ci convinciamo facilmente del fatto che la somma degli angoli di un poligono di n lati vale (n-2) angoli piatti, cioè (n-2)/2 angoli giro. Se poi il poligono di n lati è un poligono regolare, tutti i suoi angoli sono uguali tra loro e quindi ciascuno di questi angoli, espresso come frazione dell’angolo giro, vale (n-2)/2n.
Un problema significativo
Questo problema offre ai docenti l’occasione di stimolare nei propri ragazzi l’osservazione e lo studio delle figure piane (in particolare dei poligoni regolari), ma allo stesso tempo anche quella di far riflettere i propri alunni sul concetto di frazione, che è una di quelle idee forti della matematica sulle quali è bene ritornare più e più volte.
Ritornarvi chiedendo ai ragazzi di riuscire a “leggere” somme di frazioni in alcune figure dà un vantaggio, rispetto all’assegnare lunghe espressioni da semplificare: permette non solo di mantenere allenate certe abilità, ma anche di continuare a riempire di significato il concetto di frazione e di somma di frazioni.
Questa richiesta (“leggere” somme di frazioni osservando dei poligoni) rende esplicito uno dei tanti ponti tra aritmetica e geometria che frequentemente rimangono invece nascosti. Nei libri di testo della scuola del primo ciclo, ad esempio, “aritmetica” e “geometria” sono spesso trattate in sezioni rigidamente separate, se non addirittura in volumi diversi. Questa divisione impedisce agli alunni di farsi un’idea della reale unitarietà della matematica, senza rendere le cose più semplici, anzi: così facendo si rende più arduo per gli alunni cogliere certi collegamenti che, una volta percepiti, semplificherebbero la comprensione dei concetti che coinvolgono riempiendoli di significato.
Metacognizione
Accorgersi del legame tra frazioni e angoli messo in evidenza da questo problema permette agli alunni, innanzitutto, di aggiungere qualcosa alla propria rappresentazione delle frazioni e degli angoli e, quindi, di capire meglio le une e gli altri.
Ma ancora più importante è accorgersi, con questo e con altri problemi, del fatto che scoprire ponti, legami e analogie aiuta a capire meglio ciò che viene messo in relazione. Più saranno le occasioni in cui gli alunni avranno occasione di sperimentare il contributo alla comprensione dato dal notare queste analogie, maggiore sarà la probabilità che diventino essi stessi cercatori (e magari costruttori) di “ponti”.

Strategie risolutive diverse
Proprio perché si pone come ponte tra aritmetica e geometria, il problema si può affrontare con un approccio più geometrico o con uno più aritmetico.
Il suggerimento dato in calce al problema (oppure il fatto di aver precedentemente affrontato e risolto il problema Poligoni regolari e frazioni) permette di associare una frazione all’angolo interno di ciascun poligono regolare.
Si potrà dunque procedere manipolando (studiando) poligoni regolari, accostandoli intorno a un vertice a chiudere un angolo giro e quindi deducendo le corrispondenti frazioni che danno somma 1; oppure studiando (manipolando) frazioni del tipo (n-2)/2n, trovando quali di queste frazioni danno somma 1 e quindi deducendo le corrispondenti configurazioni di poligoni regolari.
In particolare i ragazzi potranno:
- manipolare un po’ di tessere di polydron [1] oppure di cartoncini a forma di poligoni regolari, preferibilmente con lo stesso lato, e procedere per tentativi;
- manipolare un po’ di tessere “virtuali” a forma di poligoni regolari, sfruttando ad esempio la piattaforma Mathigon;
- ricercare (o calcolare) le ampiezze degli angoli di alcuni poligoni regolari e cercare in quali modi si può ottenere come somma 360° (in questo caso starà all’insegnante incoraggiare i ragazzi a rileggere i loro risultati in termini di frazioni dell’angolo giro);
- scrivere un elenco di frazioni del tipo (n-2)/2n e fare un po’ di prove per vedere quali possono essere scelte per ottenere come somma 1.
È probabile che i ragazzi procedano per tentativi; e può essere significativo vederli passare da tentativi alla rinfusa ad altri sempre più ragionevoli e guidati dalle riflessioni che via via staranno facendo.
In alcune delle classi in cui questo problema è stato proposto, fornendo ai ragazzi la possibilità di usare le tessere di polydron[1] o le tessere “virtuali” di Polypad, alcuni gruppi di alunni si sono limitati a registrare tutte le situazioni in cui “a occhio” le tessere che avevano accostato completavano un angolo giro attorno a un certo vertice.
Questo ha portato gli alunni a fornire anche alcune risposte sbagliate, dovute al fatto che, nella realtà, accostando tessere di cartoncino o di Polydron o virtual, non possiamo accorgerci della differenza – per esempio – fra un angolo di 360° e uno di 359° o di 361°.Naturalmente, queste risposte sbagliate sono state una preziosa occasione per riflettere sul fatto che non tutto ciò che sembra di poter dedurre immediatamente da ciò che vediamo realizzarsi in un modello (in questo caso le tessere di cartoncino, di Polydron o virtuali) corrisponde a ciò che davvero accade agli oggetti matematici astratti (in questo caso i poligoni). Gli errori commessi (alcuni dei quali riportiamo nelle seguenti immagini) hanno anche permesso agli alunni di capire che la richiesta del problema di “leggere nelle figure delle somme di frazioni che danno come risultato 1” suggerisce un modo per verificare se le risposte trovate empiricamente costituiscano davvero una soluzione al problema oppure no.
Una pluralità di soluzioni
A puro titolo di curiosità (e perché gli insegnanti abbiano comodamente a portata di mano un riscontro e un controllo sugli esempi che i ragazzi proporranno), riportiamo nella figura qui sotto tutte le 21 maniere in cui si può riempire con poligoni regolari l’angolo giro intorno a un punto, compresi i tre casi (che nel problema abbiamo voluto escludere) in cui i poligoni sono tutti uguali fra loro. L’etichetta presente sotto ciascun disegno indica quali poligoni regolari, e in quale ordine, troviamo girando intorno al vertice comune (ogni poligono regolare è rappresentato dal numero dei suoi lati). Per esempio: l’etichetta (3, 3, 4, 3, 4) della figura in alto a destra indica che intorno al punto arrivano, nell’ordine, due triangoli equilateri (3, 3), un quadrato (4), un triangolo equilatero (3), un quadrato (4). Dato che stiamo girando intorno a un punto, si tratta di un ordine ciclico, quindi, per esempio, al posto di (3, 3, 4, 3, 4) potremmo anche scrivere (3, 4, 3, 4, 3).
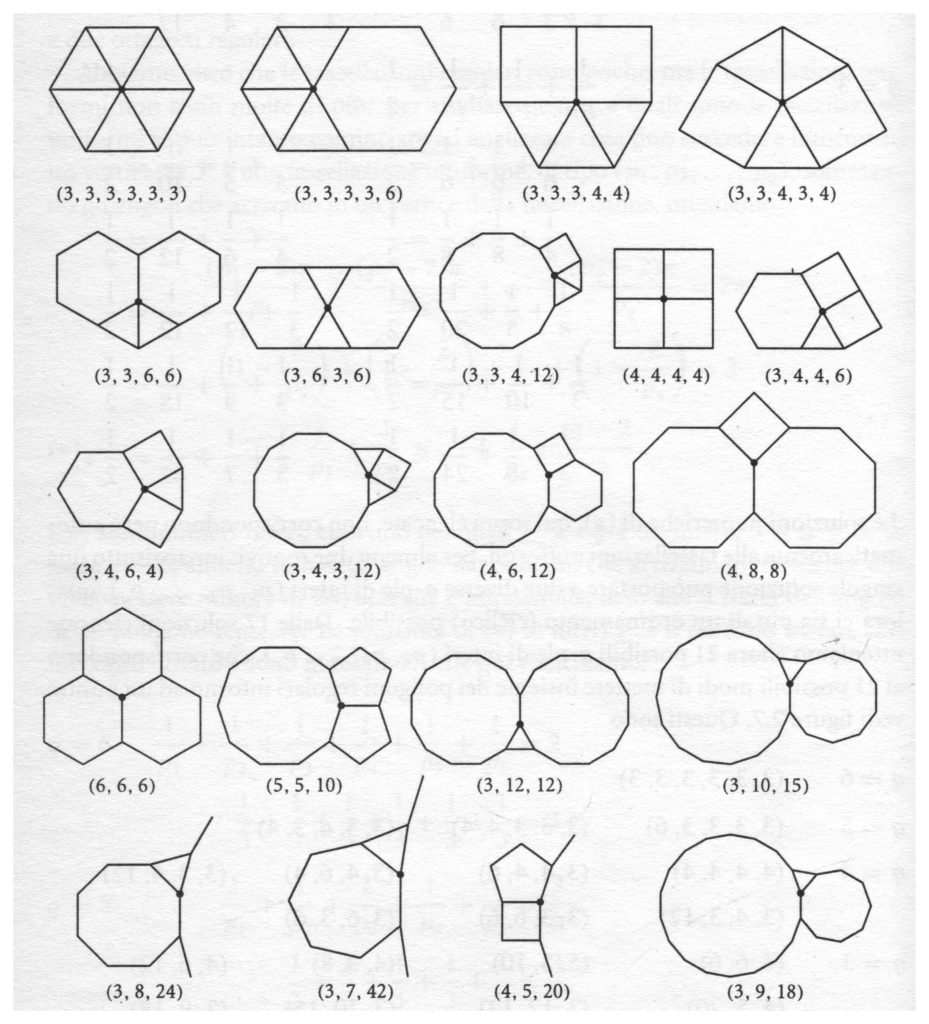
A ciascuno dei disegni in figura corrisponde un modo di scrivere 1 come somma di frazioni del tipo (n-2)/2n. Per esempio, poiché l’angolo del triangolo equilatero è 1/6 dell’angolo giro e l’angolo del quadrato è 1/4 dell’angolo giro, al disegno in alto a destra con l’etichetta (3, 3, 4, 3, 4) corrisponde la scrittura 1/6+1/6+1/4+1/6+1/4 = 1. E analogamente, poiché l’angolo dell’ottagono regolare è 3/8 dell’angolo giro e quello di un poligono regolare con 24 lati è 11/24 dell’angolo giro, al disegno in basso a sinistra con l’etichetta (3, 8, 24) corrisponde la scrittura 1/6+3/8+11/24=1. Allo stesso modo si può procedere in tutti gli altri casi.
Vale la pena notare che, dicendo che l’etichetta indica quali poligoni regolari incontriamo (e in quale ordine) girando intorno a un vertice, stiamo implicitamente dicendo che l’ordine è importante e che la soluzione contraddistinta dall’etichetta (3, 3, 6, 6) è diversa da quella etichettata come (3, 6, 3, 6). Certo che però non abbiamo esitazioni a dire che 1/3+1/3+1/6+1/6=1/3+1/6+1/3+1/6 sapendo che la somma è commutativa. Ma allora l’ordine è importante oppure no?
Questo dubbio è effettivamente emerso in alcune delle classi in cui è stato proposto il problema e il dubbio ha anche generato delle belle discussioni fra i ragazzini che sostenevano che l’ordine era importante e quelli che dicevano di no.
Il punto è che il parallelo fra poligoni regolari e frazioni va avanti solo fino a un certo punto… e per l’appunto casca sull’ordinamento: se restiamo sul terreno delle frazioni, certo non avrebbe senso distinguere tra la soluzione (3, 3, 6, 6) e la soluzione (3, 6, 3, 6) oppure tra la (3, 3, 3, 4, 4) e la (3, 3, 4, 3, 4) o ancora tra la (3, 3, 4, 12) e la (3, 4, 3, 12); invece questo ha molto senso se stiamo parlando di poligoni regolari e pavimentazioni. Ce ne accorgiamo subito osservando la figura qui sopra , ma ancora di più ce ne accorgiamo se proviamo a “continuare” la pavimentazione con la regola di rispettare in ogni vertice quella particolare assegnata successione di poligoni: in alcuni casi, come nel (3, 4, 3, 3, 4) e nel (3, 3, 3, 4, 4), possiamo continuare (anche all’infinito, a pavimentare il piano intero), ma otteniamo due pavimentazioni che non esitiamo a chiamare “diverse”.
In altri casi, poi, la differenza è ancora più marcata. Per esempio, possiamo continuare una pavimentazione (3, 6, 3, 6) accostando in ogni vertice i quattro poligoni e avendo cura di alternare un triangolo equilatero e un esagono regolare; ma provate a continuare con le stesse regole una pavimentazione (3, 3, 6, 6), cercando quindi in ogni vertice di accostare due esagoni regolari e due triangoli equilateri, mantenendo sempre questo ordine: vi accorgerete che riuscirci sarà impossibile!
Un problema aperto
Il testo del problema non parla di tassellazioni: chiede soltanto di esaminare che cosa succede intorno a un punto, senza pretendere di andare a ricoprire tutto il piano. Può succedere, però, che proprio dai ragazzi venga sollevata questa questione, magari a partire dal ricordo di pavimentazioni che può essere loro capitato di incontrare: si può estendere ciò che si è incominciato attorno a un punto fino a tassellare tutto il piano? L’immagine qui sotto è una fotografia di una porzione di pavimento di Santa Maria in Trastevere, che corrisponde a una tassellazione del piano fatta di quadrati e ottagoni regolari.
Naturalmente le due cose sono collegate: se, con un certo tipo di poligoni regolari, non si riesce a riempire l’angolo giro intorno a un punto, allora sicuramente non si riuscirà a costruire una tassellazione del piano con questi stessi poligoni regolari. Però non è detto il viceversa. Ovvero, delle 21 maniere elencate qui sopra con cui si può riempire l’angolo giro con poligoni regolari, soltanto 11 si possono estendere a una tassellazione del piano in cui in ogni vertice arrivino sempre gli stessi poligoni, nello stesso numero e nello stesso ordine: le tre regolari, cioè composte da poligoni tutti uguali fra loro (rispettivamente triangoli equilateri, quadrati, esagoni), le due già riportate nel paragrafo precedente – ossia la (3, 4, 3, 3, 4) e la (3, 3, 3, 4, 4) – e le sei che riportiamo nelle figure qui sotto.
Se consideriamo una delle altre configurazioni, per esempio quella di due pentagoni e un decagono, e cerchiamo di completarla a una tassellazione, ci accorgiamo che, girando intorno a un pentagono, tra le facce adiacenti lungo i lati di questo pentagono dovrebbero alternarsi pentagoni e decagoni; ma 5 è un numero dispari, quindi non riusciamo a chiudere il ciclo coerentemente.
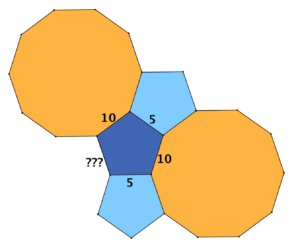
Anche negli altri nove casi si incontrano delle ostruzioni per cui ci si rende conto che è impossibile estendere la tassellazione all’intero piano. Chi è interessato può trovare una dimostrazione completa del fatto che solo 11 configurazioni su 21 si completano a una tassellazione del piano nel libro Forme. Simmetria e topologia di Maria Dedò (Decibel editrice, 1999).
Scenari possibili
La prima richiesta del problema (quella relativa all’accostare poligoni regolari non tutti uguali fra loro che riempiano l’angolo giro intorno a un punto) potrebbe essere posta, con successo, anche a ragazzini della scuola primaria.
Rispondere alla seconda richiesta (relativa al saper “leggere” nelle figure trovate delle somme di frazioni che danno come risultato 1) richiede una confidenza con le frazioni che è più facile trovare, invece, negli alunni della scuola secondaria di primo grado.
Il problema può essere interessante anche per alunni della scuola secondaria di secondo grado, in particolare se ci si vuole spingere a studiare tutte le possibili soluzioni al problema e tutte le tassellazioni regolari del piano.

Materiale necessario
Non è strettamente indispensabile, ma è sicuramente utile e opportuno che i ragazzi abbiano a disposizione del materiale costituito da poligoni regolari diversi, tutti con lo stesso lato.
A tal fine si possono usare tessere di polydron [1] o, in alternativa, si può stampare su cartoncino un congruo numero di poligoni regolari (eventualmente sfruttando i fogli allegati a fondo pagina; oppure costruendone di analoghi con GeoGebra; oppure facendoli costruire ai ragazzi stessi).
Il docente potrà valutare anche se costruire fogli con i poligoni “tutti staccati” oppure lasciare anche (come nei fogli qui allegati) il caso di poligoni che si toccano lungo un lato (con il vantaggio di ottimizzare lo spazio, ma con l’inconveniente di richiedere maggiore attenzione per il ritaglio; e inoltre il vantaggio/svantaggio di fornire già in partenza un grosso suggerimento, o addirittura la soluzione del problema se un ragazzino vispo è in grado di leggerla dalle figure).
Anche se non è strettamente indispensabile per questo problema, in vista di una possibile utilizzazione dei poligoni regolari costruiti anche per altri problemi (e in particolare per esplorare le tassellazioni piane) suggeriamo di costruirli in modo tale che abbiano tutti il lato della stessa lunghezza.
Problemi collegati
Questo problema è collegato a Poligoni regolari e frazioni, al punto che potrebbero essere considerati la prima e la seconda parte di uno stesso problema.
Note
[1] Il polydron è uno strumento, come altri esistenti in commercio, che consiste di tessere poligonali di diverse forme, con la possibilità di incastrarle fra loro.