Disegniamo alcuni rettangoli su carta a quadretti, in modo che i vertici stiano negli incroci della quadrettatura e i lati stiano sulle sue linee.
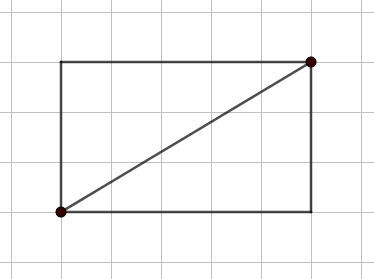
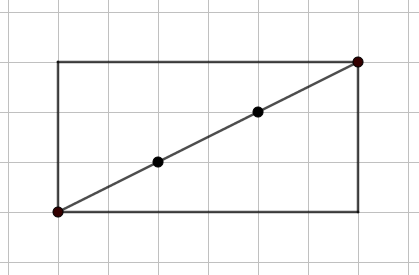
Tra questi rettangoli, chiameremo “simpatici” quelli le cui diagonali passano dagli incroci della quadrettatura solo nei vertici del rettangolo e chiameremo “antipatici” gli altri. Le diagonali dei rettangoli antipatici, quindi, passano per qualche altro incrocio della quadrettatura oltre a quelli nei vertici.
Il rettangolo in alto (che chiameremo “rettangolo 3×5” perché ha un lato di 3 quadretti e uno di 5) è un rettangolo simpatico.
Un “rettangolo 3×6” (come quello disegnato in basso) è un rettangolo antipatico.
Stabilite se sono “simpatici” o “antipatici”:
- un rettangolo 4×6;
- un rettangolo 4×7;
- un quadrato di lato 4 quadretti.
Scrivete una regola che permetta di decidere se un rettangolo con i vertici negli incroci della quadrettatura e i lati che stanno sulle sue linee è un rettangolo “simpatico” o “antipatico”, senza nemmeno doverlo disegnare, ma considerando solo i numeri naturali che esprimono le misure dei suoi lati.
Sfruttate tale regola per dare altri tre esempi di rettangoli “simpatici” e tre esempi di rettangoli “antipatici” e per stabilire se sono “simpatici” o “antipatici”:
- un rettangolo 128×189;
- un rettangolo 132×135.
Soluzione
- Un rettangolo 4×6 è antipatico.
- Un rettangolo 4×7 è simpatico.
- Un quadrato di lato 4 quadretti è antipatico.
La regola cercata può essere scritta così: un rettangolo è simpatico quando le misure dei suoi lati (rispetto alla quadrettatura) sono rappresentate da due numeri primi tra loro; negli altri casi è antipatico.
Di conseguenza:
- un rettangolo 128×189 è simpatico;
- un rettangolo 132×135 è antipatico.
Commenti
Il testo del problema lascia implicitamente intendere che, se una delle due diagonali passa per altri incroci della quadrettatura, oltre ai due estremi, anche l’altra lo fa. Non abbiamo voluto esplicitare questo fatto, immaginando improbabile che i ragazzi ne siano messi a disagio, per non appesantire ulteriormente il testo. Naturalmente, se per caso qualche ragazzo lo notasse, varrebbe la pena intanto di complimentarsi per l’attenzione nella lettura del testo e poi di esplorare insieme come un ragionamento basato sulla simmetria possa giustificare questo fatto.
Siamo di fronte ad un problema in cui il riferimento alla concretezza del foglio a quadretti potrebbe essere per certi versi un aiuto, per altri un ostacolo da superare.
Il fatto di poter iniziare ad affrontare il problema semplicemente osservando alcuni disegni fatti su carta a quadretti è senza dubbio un forte stimolo anche per chi si sente in difficoltà davanti a certe astrattezze della matematica.
Questo riferimento concreto, però, potrebbe trarre in inganno, dal momento in cui rettangoli, diagonali, punti disegnati su un quaderno sono per forza di cose una approssimazione di quelli “ideali” che hanno due, una o zero dimensioni e che quindi non corrispondono perfettamente ai disegni che ne facciamo.
Per questo motivo il testo passa abbastanza velocemente (anche rispetto ad altri Problemi per matematici in erba) dallo studio di pochi casi particolari a quello della situazione generale, onde evitare che fare troppi disegni (magari con le diagonali spesse un millimetro e i cui estremi non coincidono con i vertici del rettangolo) risulti addirittura fuorviante.
E per trovare la “regola”, anche se il testo del problema non chiede esplicitamente di argomentare, gli alunni devono passare per un ragionamento che comprenda ciò che vedono, ma vada anche “al di là”.
Un problema significativo
Questo problema tocca alcuni punti significativi del percorso di matematica nella scuola del primo ciclo, naturalmente senza la pretesa di esaurire tutto ciò che su questi temi si può fare o dire.
Un aspetto “simpatico” del problema è il fatto che lega aritmetica e geometria, due campi che troppo spesso i ragazzi ritengono due mondi differenti e distanti e che invece sono legati a corda doppia. Intanto si parte da figure sulla carta a quadretti e si arriva a formulare una regola che riguarda numeri interi, divisibilità e MCD (e, per inciso, abbiamo qui una maniera per “dare significato” a un concetto, quello del MCD, che troppo spesso i nostri ragazzi imparano solo a livello esecutivo, per poi dimenticare ben presto).
Ma c’è di più: se vogliamo andare oltre e scavare un po’ sotto la superficie del problema, ci accorgiamo che questo va a toccare il nodo della similitudine: la diagonale del rettangolo di lati m ed n è diagonale anche di tutti i rettangoli i cui lati stiano nello stesso rapporto m/n, perché tutti questi rettangoli sono simili tra loro.
È allora chiaro che questo problema ha a che fare con il concetto di rapporto e con l’equivalenza tra frazioni, ma anche – volendo guardare un po’ oltre – con l’uso di questi rapporti per descrivere la direzione di una retta disegnata su un foglio a quadretti e – andando ancora più in là – con il coefficiente angolare di una retta nel piano cartesiano.
Partendo da questo problema, ci troviamo quindi tante porte aperte in direzioni diverse: l’insegnante potrà decidere di seguirne una o l’altra, a seconda della specifica situazione della classe in cui lo propone. Ma potrà anche decidere di raccogliere questi collegamenti solo a distanza di tempo, richiamando “Rettangoli simpatici e antipatici” quando la classe affronterà temi come la similitudine o l’equazione della retta nel piano cartesiano.
Metacognizione
È possibile (forse è addirittura frequente) che alcuni gruppi non si pongano in realtà il problema descritto dal testo, ma si fermino ai numeri dati negli esempi.
Ecco allora che dai gruppi di lavoro potrebbero emergere regole come queste:
- “i rettangoli simpatici sono quelli in cui i lati sono entrambi dispari” (ed è vero che 3 e 5 sono entrambi dispari, come è vero che 3 e 6 non lo sono);
- “i rettangoli antipatici sono quelli in cui i lati sono entrambi multipli di tre” (ed è vero che 3 e 6 sono entrambi multipli di 3, mentre 3 e 5 non lo sono).
Vale la pena, dopo aver raccolto le ipotesi di “regola” date dai ragazzi, andare a verificare (qualora non l’avessero già fatto nei gruppi) se sono corrette oppure no anche facendo il disegno accurato di altri casi particolari, che consentano di riagganciarsi al problema geometrico. In certi casi un disegno in formato digitale, fatto ad esempio con GeoGebra, può essere utile perché si può andare a vedere bene che cosa succede in prossimità degli incroci della quadrettatura con una funzione di “zoom”.
A partire da queste verifiche può sorgere una discussione utilissima a proposito di esempi e controesempi e, più in generale, di come validare o confutare una regola. In altre parole, questo problema può essere l’occasione per riflettere sulle seguenti questioni:
- se trovo un esempio in cui la “regola” che ho proposto è vera, significa che ho trovato una regola vera sempre? e se trovo 10 esempi? e se ne trovo 100?
- e se tutti o quasi tutti i gruppi di lavoro hanno proposto la stessa “regola”, significa che la regola è vera? la validità di una “regola” si può stabilire con una votazione a maggioranza?
- se qualcuno mi dà un esempio in cui la “regola” che ho proposto non funziona, posso ancora dire che si tratta di una regola?
- se trovo esempi che la “regola” che ho proposto non contempla, posso ancora dire che si tratta di una regola?
Una pluralità di modi per rappresentare la soluzione
Anche se la regola per stabilire se un rettangolo “mxn” è simpatico o antipatico è sostanzialmente una sola, essa può essere scritta in tanti modi diversi, che di solito emergono nelle classi:
- il rettangolo è simpatico se il massimo comun divisore tra m e n è 1, altrimenti è antipatico;
- il rettangolo è simpatico se l’unico divisore comune di m e n è 1, altrimenti è antipatico;
- il rettangolo è simpatico se m e n sono primi tra loro, altrimenti è antipatico;
- il rettangolo è antipatico se m e n hanno dei divisori comuni diversi da 1, altrimenti è simpatico…
Non è immediato per i ragazzini riconoscere che questi e altri modi di dire sono tra loro equivalenti: uno dei compiti del’insegnante nella discussione finale è proprio quello di aiutarli a capire quali gruppi hanno detto la stessa cosa in modi diversi e quali invece hanno proposto “regole” sostanzialmente diverse.
Un problema aperto
Può essere che, una volta trovata la regola per stabilire se un rettangolo è simpatico o antipatico, negli alunni stessi sorga il desiderio di sapere da quanti incroci della quadrettatura passa la diagonale di un rettangolo antipatico, oppure (analogamente) in quanti segmenti la diagonale risulta divisa dai punti in cui passa per gli incroci della quadrettatura.
Si tratta di una domanda interessante, da non lasciar cadere nel vuoto, che sprona gli alunni ad ulteriori riflessioni su divisori, rapporti, similitudine.
Ripensiamo al primo rettangolo antipatico analizzato, il rettangolo 3×6: seguendo le suddivisioni della quadrettatura, si possono dividere entrambi i suoi lati in 3 parti uguali, perché MCD(3;6)=3.
Poiché 3=3×1 e 6=3×2, il lato più corto risulta diviso in 3 parti uguali di 1 quadretto ciascuna e il lato più lungo risulta diviso in 3 parti uguali di 2 quadretti ciascuna.
Allora il rettangolo 3×6 risulta diviso in alcuni rettangoli più piccoli, precisamente in nove rettangoli 1×2. Di questi, 3 sono posti lungo la diagonale e sono quelli che ne scandiscono la divisione in 3 parti uguali ad opera dei punti in cui essa passa dagli incroci della quadrettatura.
Quanto visto su questo esempio può essere generalizzato: il numero delle parti in cui la diagonale di un rettangolo antipatico risulta divisa dai punti in cui passa per gli incroci della quadrettatura è uguale al MCD(m;n), dove m e n sono i numeri naturali che esprimono le misure dei lati del rettangolo.
In realtà questa affermazione vale anche se il rettangolo è simpatico: in questo caso MCD(m;n)=1 e la diagonale è “tutta d’un pezzo”!
Il passaggio dal vedere in quante parti risulta divisa la diagonale allo scoprire per quanti incroci della quadrettatura essa passa è semplice: se contiamo anche i vertici del rettangolo, estremi della diagonale, questi punti saranno MCD(m;n)+1; se non li contiamo, saranno MCD(m;n)-1.
Scenari possibili
Le classi dove più naturalmente immaginiamo contestualizzato questo problema sono la prima e la seconda della scuola secondaria di primo grado. Ciò non significa che bambini di quinta primaria non potrebbero risolverlo, o che ragazzini più grandi lo troverebbero banale, ma semplicemente che questo problema ben si presta come attività utile ad affrontare alcuni temi che vedono nella prima e seconda media la loro collocazione abituale (il massimo comun divisore, la similitudine, i rapporti…).
Materiale necessario
Non è certamente indispensabile, ma può essere utile fornire agli alunni della carta centimetrata.
Può essere utile anche l’uso di un software (GeoGebra, per esempio) che permetta di costruire un rettangolo su un griglia quadrettata e di ingrandire l’immagine per vedere meglio che cosa succede in prossimità degli incroci della quadrettatura.
Problema tratto da…
“Rettangoli simpatici e antipatici” prende spunto da alcuni problemi pubblicati sul sito di Quaderno a Quadretti, proposti per le tre classi della scuola secondaria di primo grado nella prima tappa dei giochi del 2004.




