Luca è arrivato in classe l’altro giorno con questi due disegni, e ci ha raccontato che il suo amico Michel, che abita a Parigi e che è venuto a trovarlo nelle vacanze di Natale, gli ha detto che nella sua classe ne hanno costruiti tantissimi per via di un problema di geometria e che poi li hanno appesi alla parete per decorare la classe.
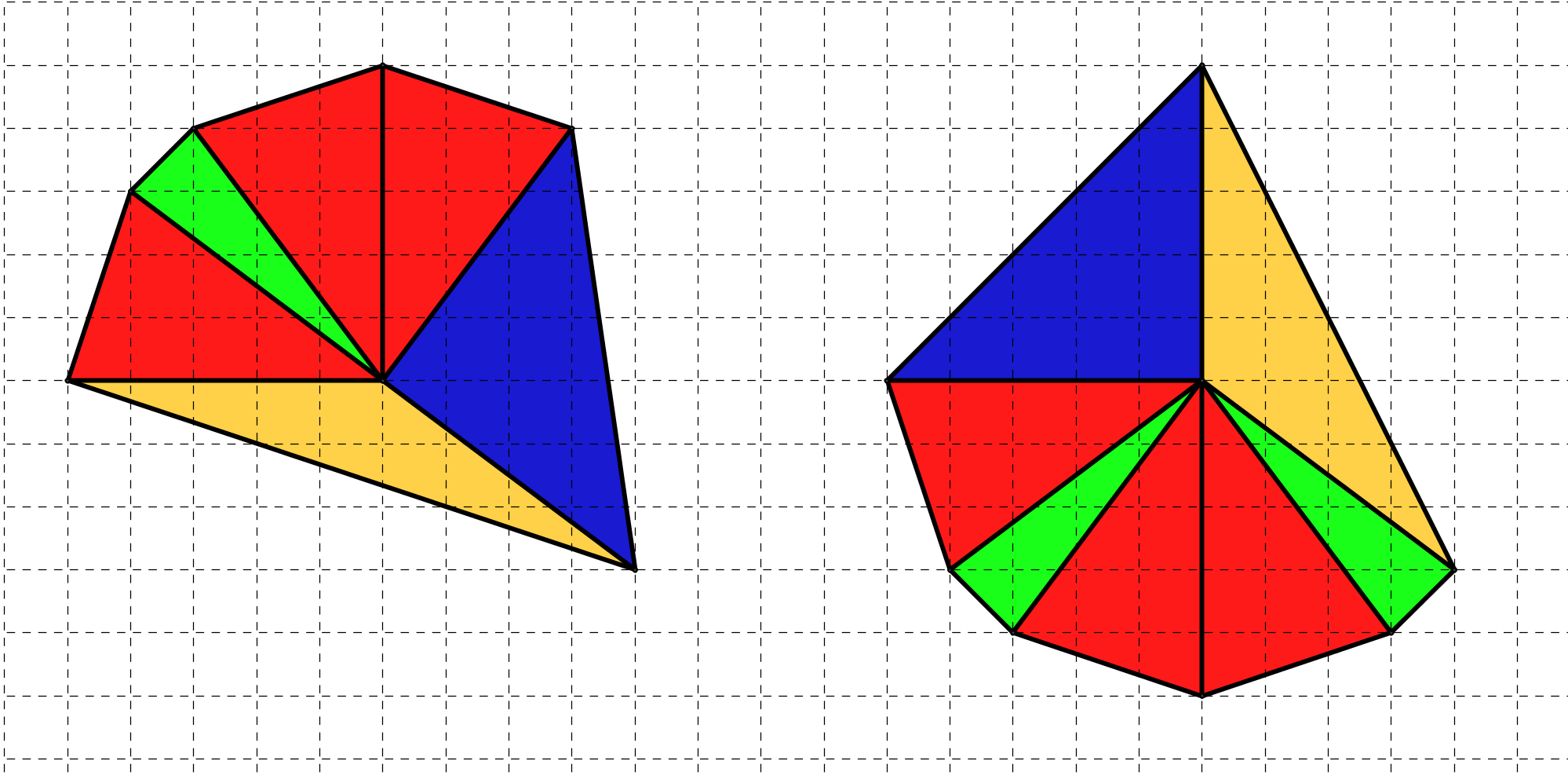
Sofia ha obiettato che le sembravano un po’ bruttini per fare da decorazioni, ma Luca le ha risposto che lei diceva così (e non aveva tutti i torti…) perché erano solo due, ma, nella foto che Michel gli ha fatto vedere, alla parete ce n’erano tantissimi, sembravano tutti di forme diverse, erano di colori molto vivaci e facevano proprio un bel vedere. E poi naturalmente siamo tutti d’accordo sul fatto che “noi siamo più bravi di loro e ne faremo di molto più belli!”.
Luca aggiunge che Michel gli aveva spiegato che il problema di geometria imponeva però delle regole molto precise per la costruzione di questi disegni:
- sono disegnati sulla carta a quadretti e sono tutti ottenuti accostando tanti triangoli isosceli;
- questi triangoli isosceli hanno tutti e tre i vertici negli incroci della quadrettatura, hanno i due lati uguali che sono lunghi esattamente 5 quadretti, e hanno tutti in comune il vertice dove si toccano i due lati uguali.
Michel gli ha detto anche che occorre tener conto del fatto che, in un triangolo rettangolo che ha due cateti lunghi 3 e 4 quadretti, l’ipotenusa è esattamente di 5 quadretti (proprio esattamente, non soltanto più o meno).
A questo punto vogliamo provare anche noi e come prima cosa abbiamo pensato che poteva farci comodo avere a disposizione il maggior numero possibile di triangoli isosceli diversi, disegnati sulla carta a quadretti e con i due lati uguali lunghi 5 quadretti (poi, di ciascuno potremo ritagliare un po’ di copie e provare ad accostarli per ottenere dei disegni più belli dei due che ci ha fatto vedere Michel).
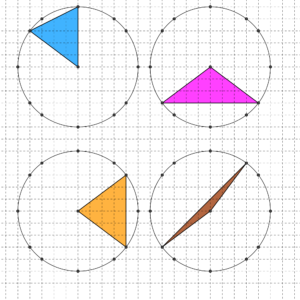
Non è facile però capire quanti triangoli isosceli, tutti diversi, si possono fare con queste regole. Per esempio, cominciamo a osservare i triangoli nelle due figure qui sopra:
- i due triangoli blu sono uguali o sono diversi?
- e i due triangoli gialli sono uguali o sono diversi?
- e tutti gli altri? sicuramente quelli verdi sono più piccoli di quelli rossi, ma siamo sicuri che quelli verdi siano tutti uguali fra loro?
- e che anche quelli rossi siano tutti uguali fra loro?
Ci domandiamo se si possono trovare altri triangoli con queste caratteristiche: sapreste suggerirci qualche altro triangolo isoscele con due lati lunghi proprio 5 quadretti, che sia diverso da tutti quelli che compaiono in queste due figure?
Ricordatevi che tutti i vertici devono essere negli incroci della quadrettatura!
Soluzione
I due triangoli blu sono triangoli rettangoli isosceli, uguali tra loro.
I due triangoli gialli sono due triangoli ottusangoli diversi.
Fra gli altri triangoli, tutti i verdi sono uguali tra loro e tutti i rossi sono uguali tra loro.
Ci sono altri quattro triangoli con le caratteristiche richieste dal problema, diversi tra loro e diversi da quelli presenti nei disegni a corredo del testo.
Commenti
Sulla lunghezza del testo
Il primo commento, quasi ovvio, riguarda la lunghezza del testo. È un testo molto lungo, che probabilmente darà del filo da torcere ai ragazzi: dal testo lungo devono capire bene qual è la situazione, quali sono le condizioni alle quali devono sottostare i triangoli di cui si parla e che cosa viene chiesto esattamente.
Avremmo potuto formulare il problema in poche righe (come in poche righe è formulato il problema “gemello” di questo, riguardante i rombi, le cui richieste sono del tutto analoghe):
Trovate sulla carta a quadretti il maggior numero possibile di triangoli isosceli che abbiano i vertici negli incroci della quadrettatura e i due lati uguali lunghi cinque quadretti. Tenete conto che la diagonale di un rettangolo di lati 3 e 4 quadretti è lunga esattamente 5 quadretti.
La narrazione di contorno (che rende il testo così lungo) ha naturalmente l’obiettivo di creare maggior coinvolgimento nei ragazzi e motivarli nella ricerca (un problema “asettico”, non contestualizzato, è più adatto per qualcuno che sia già motivato a risolvere il problema).
Ma questa non è l’unica ragione del testo così lungo; la storia consente anche di suddividere il problema in “passi” successivi l’uno all’altro, in modo da facilitare le cose: prima di chiedere ai ragazzi di trovare tutti i triangoli di quel tipo, si danno degli esempi di triangoli isosceli con i vertici nella quadrettatura e con i due lati uguali lunghi cinque quadretti, si mettono a disposizione degli alunni un po’ di esempi da osservare e sui quali ragionare, li si conduce a scoprire quali sono uguali e quali sono diversi.
Sul cuore del problema
Il vero cuore di questo problema è legato al concetto di uguaglianza e quindi alla speranza che il problema susciti discussioni tra i ragazzi, su quali triangoli sono uguali tra loro e quali sono diversi.
In questo senso, il commento a proposito del fatto che un segmento lungo 5 quadretti (grazie al triangolo rettangolo di lati 3, 4 e 5) si ritrova sulla carta quadrettata anche “in obliquo” è stato aggiunto sia affinché il problema possa essere affrontato anche da chi non conosce il teorema di Pitagora, sia allo scopo di non distrarre dall’obiettivo principale del problema l’attenzione degli alunni che già lo hanno a disposizione .
Sulla scelta dei 5 quadretti
Perché si sono scelti triangoli isosceli con i lati uguali lunghi proprio 5 quadretti? Si tratta di una scelta comoda, proprio perché (3, 4, 5) è una terna pitagorica.
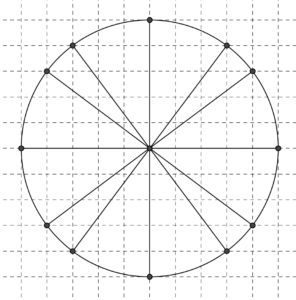
Una circonferenza con centro in un incrocio della quadrettatura e raggio pari ad un numero intero di quadretti, passa sempre per almeno 4 incroci (per capirci, associando alle righe dei quadretti le direzioni nord-sud ed est-ovest: un punto sarà a nord del centro, un altro a sud, un altro a est e un altro ad ovest).
Ma se prendiamo sulla carta a quadretti una circonferenza con centro in un incrocio della quadrettatura e raggio 5 quadretti, essa passa non solo per questi 4 incroci, ma anche per altri 8. In particolare, immaginando di inserire la circonferenza in un sistema di assi cartesiani con origine nel centro della circonferenza e con assi paralleli alle linee della quadrettatura, essa passerà anche per gli 8 punti di coordinate intere:
(3;4) (4;3), (4;-3), (3;-4), (-3;-4), (-4;-3), (-4;3), (-3;4).
Quindi, tenendo conto anche dei quattro punti di cui si diceva prima, ossia dei punti di coordinate (0;5), (5;0), (0;-5) e (-5;0), questa circonferenza passa per 12 incroci della quadrettatura.
Tutti i triangoli del problema, quindi, hanno a che fare con questo disegno: ciascuno di essi è uguale a un triangolo che ha un vertice nel centro della circonferenza e gli altri in due dei 12 punti segnati sulla circonferenza.
A domanda, risposta
I due triangoli blu sono uguali o sono diversi?
Uno dei triangoli blu dati nel testo ha i lati paralleli alla quadrettatura, quindi è un triangolo rettangolo. Ma l’altro? Se si riesce a dimostrare che anche l’altro è un triangolo rettangolo, il gioco è fatto, perché se due triangoli rettangoli hanno uguali i cateti (e questi li avrebbero tutti di 5 quadretti) allora sono necessariamente uguali.
Si possono usare vari sistemi per vedere che il triangolo blu con i lati “che non assecondano” la quadrettatura è un triangolo rettangolo.
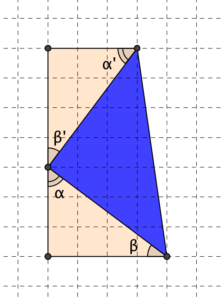Costruire altri due triangoli rettangoli con i cateti paralleli alle linee della quadrettatura può essere utile per accorgersi che anche il triangolo blu “storto” è un triangolo rettangolo.
I due triangoli rettangoli aggiunti nella figura qui accanto sono uguali fra loro perché hanno i cateti uguali (uno di 3 e l’altro di 4 quadretti). Di conseguenza sono uguali anche gli angoli: α=α’ e β=β’. Ma sappiamo che α e β sono complementari, perché sono gli angoli acuti di un triangolo rettangolo. Di conseguenza anche α e β’ sono complementari (perché β’=β). Ora, se da un angolo piatto si tolgono due angoli complementari, quello che resta è un angolo retto e di conseguenza possiamo dire che il triangolo blu è un triangolo rettangolo.
Se questa argomentazione per noi insegnanti non è complicatata, potrebbe però esserlo per i ragazzi. Essi, in realtà, hanno a disposizione anche altri modi per argomentare.
Ad esempio, chi conosce il teorema di Pitagora potrebbe verificare che il quadrato del terzo lato del triangolo blu è uguale a 50 (perché è l’ipotenusa di un triangolo rettangolo che ha un cateto di 1 quadretto e l’altro di 7 quadretti) e quindi stabilire che si tratta di un triangolo rettangolo (essendo 50=25+25=52+52); o anche, senza preoccuparsi del fatto che sia o meno un triangolo rettangolo, osservare che ha i tre lati uguali a quelli dell’altro triangolo blu con i lati sulle rette della quadrettatura.
I due triangoli gialli sono uguali o sono diversi?
Argomentare in relazione al fatto che i due triangoli gialli, ottusangoli, sono uno diverso dall’altro è più semplice, rispetto a dimostrare che i due triangoli rettangoli blu sono uguali tra loro.
Potrebbe addirittura bastare una costruzione empirica (come disegnare i triangoli su un foglio di carta e ritagliarli). Questa “argomentazione empirica” potrebbe non essere una argomentazione, ma può diventarlo se i due triangoli sono clamorosamente diversi, come in questo caso. L’angolo ottuso di un triangolo è “molto diverso” dall’angolo ottuso dell’altro; così come il terzo lato di un triangolo è “molto diverso” dal terzo lato dell’altro.
Quando c’è una differenza consistente, questo confronto empirico può bastare. Quando invece le due figure si assomigliano molto, non si può decidere se sono uguali o diverse solo dal confronto empirico (e da qui deriva la sottolineatura, nel testo, che ci riferisce a uguaglianze “esatte”, non soltanto più o meno).
E gli altri triangoli sono uguali o diversi?
Il testo del problema assume che i triangoli verdi siano più piccoli di quelli rossi e chiede se si può essere sicuri che i triangoli verdi siano tutti uguali fra loro e che anche quelli rossi siano tutti uguali tra loro.
La risposta è sì e lo si può vedere, per esempio, andando a considerare il terzo lato.
Per tutti i triangoli verdi, il terzo lato è la diagonale di un quadretto, quindi sono tutti triangoli uguali fra loro.
Per tutti quelli rossi, il terzo lato è la diagonale di un rettangolo formato da tre quadretti accostati, quindi anche questi sono tutti triangoli uguali fra loro.
Non è escluso che qualche gruppo di ragazzini provi a rispondere a questa domanda in un modo più astratto, andando a considerare le rotazioni che mandano questi triangoli l’uno nell’altro.
Nella figura iniziale, la disposizione dei triangoli “a ruota”, tutti con un vertice in comune, aiuta a intuire l’ubicazione di un possibile centro di rotazione.
Ci saranno altri triangoli con queste caratteristiche?
Infine, si chiede se ci sono degli altri triangoli con le caratteristiche richieste (anche se non si chiede quanti sono in tutto i triangoli diversi con queste caratteristiche, né si chiede di trovarli tutti).
Finora i ragazzi dovrebbero averne trovati 5, già presenti nelle figure che hanno avuto a disposizione con il testo:
- due triangoli acutangoli diversi fra loro;
- un triangolo rettangolo (in blu);
- due triangoli ottusangoli diversi fra loro.
Ce ne sono altri quattro, diversi dai precedenti e diversi tra loro.
È probabile che i ragazzi trovino facilmente i due triangoli che hanno la base del triangolo isoscele parallela alle linee della quadrettatura, ma è possibile che trovino anche gli altri.
Sperimentazione e possibili scenari
Questo problema è stato sperimentato nel corso MathUp “Problemi e approfondimenti” per la Scuola secondaria di primo grado nell’anno scolastico 2018 / 2019.
Proprio alla luce di questa sperimentazione sono state apportate delle (piccole) modifiche rispetto al testo inizialmente previsto.
Ci pare che possa essere proposto (con l’inciso relativo al fatto che “in un triangolo rettangolo che ha due cateti lunghi 3 e 4 quadretti, l’ipotenusa è esattamente di 5 quadretti”) in tutte le classi in cui si voglia far emergere una discussione autentica a proposito di quando due triangoli sono uguali e quando sono diversi.
A seconda dell’età (e non solo) dei ragazzi a cui il problema verrà proposto, ci si può aspettare una diversa sensibilità nell’argomentare le proprie risposte; la necessità di argomentare sarà, probabilmente, tanto più sentita quanto più ci saranno pareri inizialmente discordanti rispetto all’uguaglianza di due o più triangoli.
Un altro elemento che potrebbe variare sensibilmente da classe a classe è la curiosità che il problema potrà suscitare negli alunni. Alcuni ragazzi potrebbero accontentarsi di trovare uno o due triangoli (diversi da quelli già inseriti nei disegni a corredo del testo del problema) con le caratteristiche richieste, altri potrebbero anche mettersi a cercare tutti i triangoli con queste caratteristiche, magari addirittura provando ad argomentare che non ce ne sono altri.
Quadretti grandi, quadretti piccoli
Una questione emersa durante la sperimentazione, e che potrebbe ripetersi nelle classi che affronteranno questo problema in futuro, riguarda le dimensioni dei quadretti.
Potrebbe succedere che i quadretti della carta che gli alunni avranno a disposizione siano diversi da quelli dei disegni stampati insieme al testo del problema. Eventuali errori, dubbi o proteste dovute a questa discrepanza potrebbero essere preziosi per sottolineare ai ragazzi un fatto importante (che è in realtà contenuto nel testo, ma in maniera un po’ nascosta): le figure in questo problema indicano (soltanto!) come il triangolo in questione è disposto rispetto alla quadrettatura.
Quindi, se si volesse confrontare direttamente due triangoli (ad esempio usando il righello) per decidere se sono uguali o sono diversi, occorrerebbe disegnarli sulla stessa quadrettatura.
Peraltro – e questo è un punto importante di cui sarebbe opportuno rendere consapevoli i ragazzi – in questo problema l’uso del righello è proprio inopportuno: e questo è implicitamente suggerito dal testo quando si sottolinea quel “proprio esattamente, non solo più o meno”.
Il righello ci dà sempre comunque (solo) una misura, che non può che essere una valutazione “più o meno”, una valutazione approssimata; il riferimento alla quadrettatura, o al teorema di Pitagora (sia che lo sappiamo, sia che ci venga garantito dall’insegnante) ci dà invece una valutazione esatta.
Come scriveva una corsista MathUp, nel vedere i ragazzi all’opera di fronte a problemi come questo ci si rende davvero conto del fatto che
misurare è diverso da calcolare!
I vertici negli incroci dei quadretti
Uno degli errori più frequentemente commessi dagli alunni delle classi che, durante la sperimentazione legata ai corsi MathUp, hanno affrontato questo problema è stato il fatto che i vertici dei triangoli spesso erano messi a casaccio, come se i ragazzi non si fossero accorti della richiesta che i vertici dovessero stare negli incroci della quadrettatura.
Poiché nel testo questa richiesta è esplicita ed è illustrata anche da numerosi esempi, ci viene da pensare che i ragazzi semplicemente non l’abbiano ritenuta degna di attenzione. Forse sono abituati a non dare importanza a dove fanno i disegni, forse non hanno mai avuto occasione di riflettere sulle potenzialità e i limiti della carta a quadretti, sta di fatto che hanno sicuramente letto la richiesta contenuta nel testo, ma in molti non l’hanno tenuta in considerazione.
Per questo motivo ci pare utile che, almeno in quelle classi in cui i ragazzi non hanno mai lavorato su poligoni ai cui vertici fosse imposto di stare negli incroci di una quadrettatura, venga quantomeno mostrato un geopiano. Se poi la classe ne avesse a disposizione uno per gruppo, la ricerca dei triangoli potrebbe iniziare con questo strumento: già solo il fatto di “ricopiare” sulla carta a quadretti un poligono costruito sul geopiano fa toccare con mano cosa significhi la richiesta che i vertici devono stare negli incroci della quadrettatura.
Materiale necessario
Sarà naturalmente necessario che i ragazzi abbiano a disposizione della carta a quadretti.
Uno strumento che (pur non essendo assolutamente “necessario”) potrebbe aiutare i ragazzi a porre attenzione al fatto che, in questo problema, si chiede che i triangoli abbiano i vertici negli incroci della quadrettatura è il geopiano.
Problema tratto da…
Questo problema è tra quelli proposti nella sperimentazione legata al corso MathUp “Problemi e approfondimenti” per la Scuola secondaria di primo grado nell’anno scolastico 2018 / 2019.
Problemi collegati
Si tratta di un problema analogo a “Rombi sul quaderno a quadretti“.
